Compression

CS240E: Data Structure and Data management (Enriched)

David Duan, 2019 Winter, Prof. Biedl

Encoding Basics

Motivation

Problem How to store and transmit data?

• Source Text: The original data, string $S$ of characters from the source alphabet $\Sigma_S$.
• Coded Text: The encoded data, string $C$ of characters from the coded alphabet $\Sigma_C$.
• Encoding: An algorithm mapping source texts to coded texts.
• Decoding: An algorithm mapping coded texts back to their original source text.

Measuring Performance

The main object for compression is to make $|C|$ small.

We look at the compression ratio $\displaystyle \frac{|C|\cdot \log|\Sigma_C|}{|S|\cdot \log|\Sigma_S|}$.

In this course, we usually let $\Sigma_C = \{0, 1\}$, and we focus on physical, lossless compression algorithm, as they can safely be used for any application.

Fixed-Length Encoding/Decoding

Fixed-length encoding makes the decoding process easy, as we could break $C$ into pieces and translate each piece back to the original. However, the compression ratio is not optimal.

Example: Caesar Shift, ASCII

Variable-Length Encoding/Decoding

More frequent characters get shorter codewords.

Example: Morse Code (which can be represented as a trie), UTF-8 encoding (which can handle more than 107000 characters using only 1 to 4 bytes).

Prefix-Free

Note that Morse code is not uniquely decodable; it uses additional pauses to avoid ambiguity.

The prefix property requires that there is no whole code word in the system that is a prefix (initial segment) of any other code word in the system. From now on, we only consider prefix-free codes (codes with the prefix property), which corresponds to a trie with characters of $\Sigma_S$ only at the leaves.

The codewords need no end-of-string symbol $\$$ if the code is prefix-free.

Decoding of Prefix-Free Codes

Any prefix-free code is uniquely decodable.

Runtime: $O(|C|)$. Note that $i$ is incremented in the inner while loop. Intuitively, each character we consumed corresponds to one step traversing the trie.

Encoding From the Trie

We can also encode directly from the trie.

Runtime: $O(|\Sigma_S| + |C|)$.

Huffman Encoding

Youtube resource:

• Concise: https://www.youtube.com/watch?v=dM6us854Jk0
• Detailed: https://www.youtube.com/watch?v=ikswC-irwY8 (Stanford)

Motivation

Consider $S = LOSS$ with prefix-free codes

                                         *
                                      0     1
                                    *         *
                                  0   1     0   1
                                 L     O   E     S      

Then the encoded text will be $00 \; 01 \; 11 \; 11$. Observe the length of the code word $|C|$ is

To minimize $|C|$, we want to put the infrequent characters "low" in the trie.

Huffman encoding is a greedy algorithm which gives us the "best" trie that minimizes $|C|$.

Procedure

Strategy

We build a mini-trie using two least-frequent characters and treat this trie as a single character with the sum of two children's frequencies being its frequency. Repeat this process until we have exhausted all used characters.

Note that we need to return both encoded text and trie/dictionary, because otherwise we can't decode the text as the algorithm may return many variations of the trie (not unique).

Pseudocode

Analysis

Huffman Code uses two passes: building frequency array and building min-heap.

Huffman Code is not "optimal" in the sense that it

1. ignores the fact that we need to send an additional trie, and
2. assume we use character-by-character encoding

A correct statement is, Huffman encoding finds the prefix-free trie that minimizes $|C|$.

Proof: Huffman returns the "best" trie

We do induction on $|\Sigma_S|$. We want to show that $T_H$ constructed using Huffman satisfies $C(T_H) \leq C(T)$ for any trie $T$ that encodes $S$.

Base Case: $|\Sigma_S| = 2$, call them $\{a, a'\}$. Then Huffman returns

xxxxxxxxxx
                                           *
                                         /   \
                                        a     a'            

which is the best possible trie.

Step: We know $T_H$ has the above mini-trie at the bottom. Consider a differen trie $T$ with $b$ and $b'$ be the characters that are at the lowest level; $a$ and $a'$ are somewhere else.

• Suppose $\{a, a'\} = \{b, b'\}$, if we remove them, then both $T_H'$ and $T'$ give tries for alphabet $\Sigma_s'= \Sigma_S - \{a,a'\} \cup \{c\}$ where $freq(c) = freq(a) + freq(a')$. Observe $T_H'$ is the Huffman trie for $\Sigma_S'$. By IH $C(T'_H) \leq C(T')$, we get

  $$C(T_H) = C(T'_H) + f(a) + f(a') \leq C(T') + f(a) + f(a') = C(T).$$

• Otherwise, switch $\{b, b'\}$ with $\{a, a'\}$ in $T$ and argue on the resulting tree. Details skipped. $\square$

Runtime Analysis

• Encoding: $O(|\Sigma_S| \log |\Sigma_S| + |C|)$.

  • Build frequency array takes $O(|S|)$.
  • Build min-heap takes $O(|\Sigma_S| \log |\Sigma_S|)$.
  • Build decoding trie takes $O(|\Sigma_S| \log |\Sigma_S|)$.
  • Encoding takes $O(|\Sigma_S| + |C|)$.

• Decoding: $O(|C|)$ (see 1.4.2).

Exercises

1. Huffman is a [ single / multi ] - chararcter encoding algorithm.
2. Huffman uses [ fixed / variable ] - length codeword.
3. Huffman requires [ 1 / 2 / 3 ] passes through the text.
4. Describe the procedure before constructing the final trie.
5. Describe the procedure for constructing the final trie.
6. Analyze the runtime for each step of Q4 & Q5 solutions.
7. What is the main goal of Huffman encoding?
8. Is the trie returned by Huffman unique? Does this have any implication?
9. Given the following frequency array, produce a Huffman trie with $\Sigma_C = \{0,1\}$: {'A':10, 'E':15, 'I':12, 'S':3, 'T':4, 'P':13, '\n':1}.
10. What's the ideal scenario to use Huffman encoding?

Solution

1. Single: looking at frequency of each individual character.
2. Variable: codewords correspond to leaves with different depth in a trie.
3. 2 (one for building trie, one for actual encoding).
4. Loop through the input text $S$ and build an array of frequencies $f$ indexed by $s \in \Sigma_S.$
5. Initialize an empty min-heap $Q$; for each $s \in \Sigma_S$, insert a singleton tree to $Q$ with frequency $f[s]$ representing $s$; while $Q$ has more than one tree, pop the two trees with least frequencies, build a new tree using them as children, set the frequency as their sum; when this ends, we are left with a single tree inside $Q$ that represents the optimized trie.
6. Build frequency array takes $O(|S|)$; build min-heap takes $O(|\Sigma_S| \log |\Sigma_S|)$; build decoding trie takes $O(|\Sigma_S| \log |\Sigma_S|)$; encoding takes $O(|\Sigma_S| + |C|)$.
7. Find the prefix-trie that minimizes $|C|$.
8. No, not unique; because of this, we need to return both the encoded text and the trie from the algorithm.
9. Solution not unique; watch first youtube video for one possible solution.
10. Huffman is good when the frequencies of characters are unevenly distributed.

Run-Length Encoding

Strategy

Variable-length & multi-character encoding: multiple source-text characters receive one code-word; the source and coded alphabet are both binary $\{0, 1\}$; decoding dictionary is uniquely defined and not explicitly stored.

Elias Gamma Code

We encode $k$ with $\lfloor \log k \rfloor$ copies of $0$ followed by the binary representation of $k$, which always starts with $1$:

Encoding

Example

$S = 11111110010000000000000000000011111111111$.

1. $C[0] = 1$.
2. Block of $1$'s with length $7$: $00111$.
3. Block of $0$'s with length $2$: $010$.
4. Block of $1$'s with length $1$: $1$.
5. Block of $0$'s with length $20$: $000010100$.
6. Block of $1$'s with length $11:$ $0001011$.

Thus: $C = 10011101010000101000001011$.

Pseudocode

Decoding

Example

$C = 00001101001001010$

1. First bit $b = 0$, so current bit is $0$.
2. Followed by $000$, so we know the block has length $8 \leq k < 16$. We read $1101$ and get $13$, so we append $13$ zeros to $S$.
3. Next, $00$, so we know the block has length $4 \leq k < 8$. We read $100$ and get $4$, so we append $4$ ones to $S$.
4. Next, there is no zero, just a one, so we know the next block is just a single zero; append $1$ zero to $S$.
5. Next, $0$, so we know the block has length $2 \leq k < 4$. We read $10$ and get $2$, so we append $2$ ones to $S$.

As a remark, let $l$ denote the number of zeros we encounter during each iteration, note that we always read $l+1$ bits to get the length of current block.

$S = 00000000000001111011$.

Pseudocode

Analysis

This works very well for long runs. For example, if your string is $n$ zeros, then you can use $2 \lfloor \log n \rfloor + 2$ zeros to represent the string:

1. One leading $0$ to denote it is a zero block,
2. $\lfloor \log n \rfloor$ leading zeros for the run,
3. $\lfloor \log n \rfloor + 1$ bits to represent the length in binary.

However, RLE works poorly when there are many runs of length $2$ or $4$, because the encoded text might be even longer than the original text. To see this, observe you need three bits to represent a block of length two and five bits to represent a block of length four. In fact, up to $k=5$, you at most do as well as before.

Thus, this is bad for random bitstring, but good for sending pictures with a lot of white with a few block spots.

Exercises

1. RLE is a [ single / multi ] - chararcter encoding algorithm.
2. RLE uses [ fixed / variable ] - length codeword.
3. RLE requires [ 1 / 2 / 3 ] passes through the text.
4. Describe Elias Gamma Code (hint: two parts).
5. Describe the encoding procedure.
6. Describe the decoding procedure.
7. During decoding, if we find $l$ initial zeros, how many bits do we need to read afterward?
8. What's the best case performance for RLE?
9. When is RLE good / bad?
10. What's the ideal scenario to use RLE?

Solution

1. Multi: it works on a block of code.
2. Variable: depends on Elias Gamma code.
3. One pass only.
4. For a block of length $k$, Elias Gamma code is $\lfloor \log k \rfloor$ followed by $k$ in binary.
5. The first bit tells the bit of the first block; concatenate the Elias Gamma code for each block to produce $C$.
6. The first bit tells the bit of the first block; if see a block of $l$ zeros, read the following $l+1$ bits and denote it as the length of the block.
7. $l+1$ bits.
8. A block of $n$ zeros can be encoded using $2 \lfloor \log n \rfloor + 2$ zeros.
9. Good: pictures with a lot of whites and a few black spots; bad: random bit strings. In particular, up to length $k=5$, you at most do as well as the original text.
10. RLE is good when there are long runs.

Lempel-Ziv-Welch

Huffman and RLE mostly take advantage of frequent or repeated single characters, but we can also exploit the fact that certain substrings show up more frequently than others. The LZW algorithm encodes substrings with code numbers; it also finds substrings automatically. This is used in compress command and GIF format.

Strategy

Always encode the longest substring that already has a code word, then assign a new code word to the substring that is 1-bit longer.

Adaptive Encoding

In ASCII, UTF-8, and RLE, the dictionaries are fixed, i.e., each code word represent some fixed pattern (e.g., $65 \leftrightarrow A$). In Huffman, the dictionary is not fixed, but it is static, i.e., the dictionary is the same for the entire encoding/decoding process (we compute the frequency array beforehand).

However, in LZW, the dictionary is adaptive:

• We start with a fixed initial dictionary $D_0$, usually ASCII.
• For $i \geq 0$, $D_i$ is used to determine the $i$th output character.
• After writing the $i$th character to output, both encoder and decoder update $D_i$ to $D_{i+1}$.

In short, the dictionary keeps changing after receiving new information. As a result, both encoder and decoder must know how the dictionary changes.

Encoding

Procedure

1. We store dictionary $D_i$ as a trie.
2. Parse trie to find the longest prefix $x$ already in $D_i$, i.e., $x$ can be encoded with one code number.
3. All $xK$ to the dictionary (this prefix would have been useful), where $K$ is the character that follows $x$ in $S$. This creates one child in trie at the leaf we stopped.

Example

1. Convert $A = 65$, add $AN$ to $D$ as $128$ (first available code word as ASCII uses $0$ to $127$).
2. Convert $N = 78$, add $NA$ to $D$ as $129$.
3. Convert $AN = 128$, add $ANA$ to $D$ as $130$.
4. Convert $A = 65$, add $AS$ to $D$ as $131$.
5. Convert $S = 83$, add $SA$ to $D$ as $132$.
6. Convert $AN = 128$, add $ANN$ to $D$ as $133$.
7. Convert $NA = 129$, done.

Final output: str(bin(65)) + str(bin(78)) + ... + str(bin(129)) where + denote string concatenation.

Pseudocode

Decoding

Procedure

We build the dictionary which maps numbers to strings while reading strings. To save space, store string as code of prefix plus one character. If we want to decode something but it is not yet in dictionary, we know the "new character" for this one must be the first character in its parent.

Example

1. Start with $D$ being ASCII. Convert $67$ to $C$.

2. Convert $65$ to $A$; add $CA$ to $D$ with $i = 128$.

3. Convert $78$ to $N$; add $AN$ to $D$ with $i = 129$.

4. Convert $32$ to space; add $N\underline{\phantom{1}}$ to $D$ with $i = 130$.

5. Convert $66$ to $B$; add $\underline{\phantom{1}} B$ to $D$ with $i = 131$.

6. Convert $129$ to $AN$; add $BAN$ to $D$ with $i = 132$.

7. Convert $133???$ This code number is not in $D$ yet!

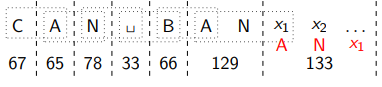
   However, we know it would be added to $D$ representing $ANx$ where $x$ is the unknown next character. After that, we would use $133$ as $ANx$. This tells us $x = A$! In general, if code number is not yet in $D$, then it encodes "previous string + first character of previous string".

Pseudocode

Analysis

Encoding: parse each character while going down in trie, so $O(|S|)$ where $S$ is the input string.

Decoding: parse each code word while going down in trie, so $O(|C|)$ where $C$ is the coded text.

Overall linear time.

Exercises

1. LZW is a [ single / multi ] - chararcter encoding algorithm.
2. LZW uses [ fixed / variable ] - length codeword.
3. LZW requires [ 1 / 2 / 3 ] passes through the text.
4. What's the biggest difference between LZW and Huffman/RLE?
5. How is the dictionary for LZW different from dictionary for Huffman?
6. Describe the procedure for encoding.
7. Describe the procedure for decoding.
8. What is the special case for decoding?
9. Analyze the runtime for LZW.
10. What's the ideal scenario to use RLE?

Solution

1. Multi: LZW work on repeated substrings.
2. Fixed: Each substring is represented by a fixed-length codeword in a dictionary (ASCII).
3. One pass: LZW parses and updates the dictionary at the same time.
4. LZW takes advantage of repeated substrings whereas Huffman and RLE take advantage of repeated characters.
5. Dictionary for Huffman is static, that is, it is fixed once it is built; dictionary for LZW is adaptive, that is, it is frequently updated using the new information given.
6. Starting with ASCII (as a trie), parse the trie to find the longest prefix that is already in $D$; append this to the output and add the prefix with the next character to $D$; repeat until run out of input.
7. Same as encoding, update the dictionary while parsing the text, unless it's the spcial case (see Q8).
8. If we want to decode something but it is not yet in dictionary, we know the "new character" for this one must be the first character in its parent. In general, if code number is not yet in $D$, then it encodes "previous string + first character of previous string".
9. Both encoding and decoding are basically parsing text while going down in a trie, so linear time.
10. LZW works well when there are repeated substrings. It is also very fast.

Summary

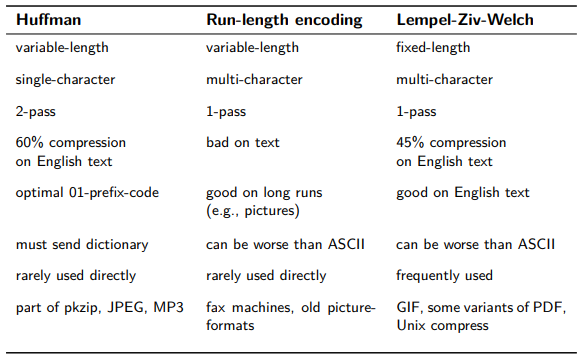
Move-To-Front Transform

Motivation

Recall the MTF-heuristic when storing a dictionary as an unsorted array. The search is potentially slow, but if we have reasons to believe that we frequently search for some items repeatedly, then the MTF-heuristic means a very fast search.

Procedures

Analysis

Input: Long Runs

Suppose the input $T_1$ has long runs of characters. We can view $T_1$ as a sequence of requests for characters in a dictionary that contains ASCII. If we store the dictionary as an unsorted array $L$ with the MTF-heuristic, we can transform $T_1$ into a sequence of integers by writing, for each such "request-character" $c$, the index where $c$ was found. In genral, if $T_1$ has a character repeating $k$ times, then $T_2$ will have a run of $k-1$ zeros. You will see this becomes useful when processing output from Burrows-Wheeler transform.

Output: Uneven Distribution

The output $T_2$ should also have the property that small indices are much more likely than larger indices, presuming we start with ASCII. This holds because the used characters are brought to the front by MTF, so if they are ever used again they should have a much smaller number. Therefore, the distribution of characters in $T_2$ (characters now means number in $\{0, \ldots, 127\}$) is quite uneven, making it suitable for Huffman encoding.

Adaptive Dictionary

MTF transform also uses adaptive dictionary, since the dictionary changes at every step. However, the change happens in a well-defined manner that only depends on the currently encoded character. Therefore, the encoder can easily emulate this, and no special tricks are needed for decoding.

Runtime

The runtime is propotional to the total time that it takes to find the characters in the dictionary, which is $O(|\Sigma_S| \cdot |S|)$ in the worst case, but in practice the performance is much better since frequently used characters should be found quickly.

Exercise

1. Explain what MTF-heuristic does.
2. When used in BZip2, what assumption do we have for its input? In other words, why do we believe that MTF would have good performance given this input?
3. Describe the procedure for encoding and decoding.
4. What is the goal for MTF? In other words, what kind of output do we hope to pass on?

Solution.

1. Upon searching for an element, move it to the front. Hence the name "MTF".
2. After BWT, there will usually be long runs of repeated characters. If we see each of them as one look-up request, searching for the same key repeatedly is very fast in MTF.
3. Starting with ASCII, search for each character and append the index where we found it to the output stream until we run out of input characters. Same for decoding, except we are outputting the characters given the index.
4. We hope to output numbers with unevenly distributed frequencies because Huffman could take advantage of that. In particular, there will be long runs of zeros if the input has long runs of repeated characters.

Burrows-Wheeler Transform

Motivation

Encoding

Cyclic Shift

Given a string $S[0\cdots n-1]$, the $i$th cyclic shift of $S$ is the string $S[i \cdots n-1] + S[0 \cdots i-1]$, i.e., the $i$th suffix of $S$, with the "rest" of $S$ appended behind it.

Strategy

Take the $n$ cyclic shifts of source text $S$, sort them alphabetically, and then output the last character of the sorted cyclic shifts.

To make BWT encoding more efficient in practice, observe the $k$th character of the $i$th cyclic shift is $S[i+k\mod n]$, so we can read any cyclic shift directly from $S$ without doing MSD radix sort.

We said to sort the cyclic shifts, but actually for extracting the encoding, all we need is to describe what the sorting would have been, or put differently, to give the sorting permutation. It turns out that it is better to have the inverse sorting permutation $\pi$ that satisfies the following: if $s_0, s_1, \ldots, s_{n-1}$ is the sorted order of cyclic shifts, then $s_i$ is the $\pi(i)$-th cyclic shift, i.e., $s_i = S[\pi(i), \pi(i)+1, \ldots, n-1, 0, 1, \ldots, \pi(i)-1]$. In consequence, the $i$th character of the encoding is $S[\pi(i) - 1]$ (or $S[n-1] = \$$ if $\pi(i) = 0$).

Pseudocode

TBC

Bzip2

Pipeline

Text $T_0$: Original Text

• BWT: If $T_0$ has repeated long substrings, then $T_1$ has long runs of characters.

Text $T_1$

• MTF: If $T_1$ has long runs of characters, then $T_2$ has long runs of zeros.

Text $T_2$

• RLE: If $T_2$ has long run of zeros, then $T_3$ has unevenly distributed input.

Text $T_3$

• Huffman: Compresses well since input-chars are unevenly distributed.

Text $T_4$: Encoded Text

Analysis

Encoding can be slow: BWT bottle-neck (recall $O(n \log n)$ if using suffix array via modified MSD radix sorting).

Decoding is fast: Both MTF and BWT can be decoded in $O(n)$ without need to anything more complicated than countsort.

Drawback: We need the entire source text at once because BWT needs to sort cyclic shifts. Thus it is not possible to implement bzip2 such that both input and output are streams, i.e., we can't use it for large text that can't fit into memory.