External Memory

CS240E: Data Structure and Data management (Enriched)

David Duan, 2019 Winter, Prof. Biedl

External Memory Model

Memory Hierarchies

Recall from CS251, computers have a hierarchy of different kinds of memories, which vary in terms of their size and distance from the CPU. Ordering from the fastest and smallest to the slowest and largest, we have registers, cache, internal memory, and external memory.

In most applications, only two levels really matter -- the one that can hold all the data items in our problem and the level just below that one. Bringing data items in and out of the higher memory that can hold all items will typically be the computational bottleneck in this case.

In this module, we adapt our algorithm to take the memory hierarchy into account, avoiding transfers as much as possible.

EMM

• Suppose internal memory has size $M$ and external memory has unlimited size.
• Fast random access between CPU and internal memory.
• Slow access (only in blocks of size $B$) between internal and external memory.
• We measure the cost of computation by the number of block transfers between internal and external memory.

External Sorting

David: This section is not being tested on the final exam.

Sorting

Given an array $A$ of $n$ numbers, we want to put them into sorted order. Assume $n$ is huge and $A$ is stored in blocks in external memory.

Recall in the RAM model, heapsort gives the optimal time ($O(n \log n)$) and space ($O(n)$) performance. However, accessing a single location in external memory automatically loads a whole block, so accessing $A$ at indices that are far apart is very costly, typically one block transfer per array access.

Mergesort, on the other hand, adapts well to an array stored in external memory. It can be made even more effectively using $d$-way merge, i.e., merging $d$ sorted runs into one sorted run.

Multi-Way Merge

Remark.

1. The standard merge (used in mergesort) uses $d = 2$.
2. We could use $d>2$ for internal memory mergesort, but the extra time for $deleteMin$ means the overall runtime is no better.

External Mergesort

Let $n$ be the number of elements in the array stored in external memory, $M$ be the size of internal memory, and $B$ be the size of block, i.e., how many elements can we transfer from external to internal memory using one block transfer.

Step I. Create $n/M$ sorted runs of length $M$.

• Loading all elements from external to internal memory takes $\Theta(n/B)$ block transfers.
• Notice sorting takes place in internal memory and we don't care about it in EMM.

Step II. Merge the first $d \approx M/B-1$ sorted runs using $d$-way-merge.

• Each of $S_1, \ldots, S_d$ inside internal memory have size $B$ because that's how many we could load using one transfer.
• $S$ also has size $B$ (this explains the $-1$) and we use it as intermediate storage inside internal memory after selecting $B$ smallest elements from $S_1, \ldots, S_d$.
• When $S$ is full, we write it back to an array (different one, we don't want to overwrite the original as we are still in progress of sorting) stored in external storage array and clear $S$.
• After the first $d$-way-merge, the first $d$ sorted runs (each of size $M$) will become a sorted run of size $Md$ stored in an array in external memory.

Step III. Keep merging the next runs to reduce the number of runs by factor of $d$.

• Again, we don't care about the $d$-way merging because it is in internal memory.
• We need $\Theta(n/B)$ block transfers to write everything back to external memory.
• Note that we need $\log_d(n/M)$ rounds of merging to create a sorted array: originally there are $n/M$ sorted runs; each iteration of $d$-way-merge reduces the number of sorted runs by a factor of $d$, hence the result.

Thus, the total number of block transfers is $O(\log_d(n) \cdot n/B)$, as we need to perform $\log_d(n/M) \in O(\log_d(n))$ rounds of $d$-way-merge and each round of merging requires $\Theta(n/B)$ block transfers (both loading and write back).

Lower Bound for External Sorting

Theorem Sorting $n$ elements stored in external memory requires

block transfers.

The ratio $M/B$ is the number of external memory blocks that can fit into internal memory. This theorem is saying that the best performance we can achieve for the sorting problem is equivalent to the work of scannign through the input set (which takes $\Theta(n/B)$ transfers) at least a logarithmic number of times, where the base of this logarithm is the number of blocks that can fit into internal memory.

As a remark, $d$-way mergesort with $d \approx M/B$ is optimal, because we are sorting as many (smaller) sorted runs as possible.

External Dictionaries

Multi-Way Search Tree

David: 3.1 is merely a motivation for the following data structures.

Let $v$ be a node of an ordered tree. We say that $v$ is a $d$-node if $v$ has $d$ children. We define a multi-way search tree to be an ordered tree $T$ that has the following properties:

1. Each internal node of $T$ has at least two children. That is, each internal node is a $d$-node, where $d \geq 2$.
2. Each internal node of $T$ stores a collection of itesm of the form $(k,x)$, where $k$ is a key and $x$ is an element.
3. Each $d$-node $v$ of $T$, with children $v_1, \ldots, v_d$, stores $d-1$ items $(k_1, x_1), \ldots, (k_{d-1}, x_{d-1})$, where $k_1 \leq \cdots \leq k_{d-1}$.
4. Define $k_0 = - \infty$ and $k_d = + \infty$. For each item $(k,x)$ stored at a node in the subtree of $v$ rooted at $v_i$, $i = 1, \ldots, d$, we have $k_{i-1} \leq k \leq k_i$.

If we think of the set of keys stored at $v$ as including the speical keys $k_0 = -\infty$ and $k_d = +\infty$, then a key $k$ stored in the subtree of $T$ rooted at a child node $v_i$ must be "in between" two keys stored at $v$. This simple viewpoint gives rise to the rule that a node with $d$ children stores $d-1$ regular keys, and it also forms the basis of the algorithm for searching in a multi-way search tree.

$(2,4)$ Tree

Let $k_i$ denote keys and $*_i$ denote pointers to subtrees.

• KVPs in subtree $*_0$ have keys less than $k_1$.
• KVPs in subtree $*_1$ have keys greater than $k_1$ but less than $k_2$.
• KVPs in subtree $*_2$ have keys greater than $k_2$ but less than $k_3$.
• KVPs in subtree $*_3$ have keys greater than $k_3$.

Properties

In using a multi-way search tree in practice, we desire that it be balanced, i.e., have logarithmic height. We can maintain balance in a $(2,4)$ tree by maintaining two simple properties:

1. Size property: every node has at most four children.

   1. $2$-node: $1$ KVP & $2$ subtrees (possibly empty).
   2. $3$-node: $2$ KVP & $3$ subtrees (possibly empty).
   3. $4$-node: $3$ KVP & $4$ subtrees (possibly empty).

2. Depth property: all the external nodes have the same depth.

   1. All empty subtrees are at the same level.

Enforcing the size property for $(2,4)$ trees keeps the size of the nodes in the multi-way search tree constant, for it allows us to represent the dictionary $D(v)$ stored at each internal node $v$ using a constant-sized array. The depth property, on the other hand, maintains the balance in a $(2,4)$ tree, by forcing it to be a bounded depth structure.

Search

Search is very similar to BST:

Insert

As in BST-Insert, we first find where the node should be added. However, the depth property does not allow the tree to grow downward, so we add it to the list of KVPs stored inside the current node (always a leaf) and perform "fix-ups" if necessary.

For example, if we insert $k=17:$

--->

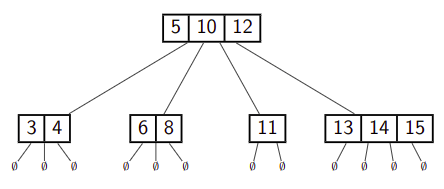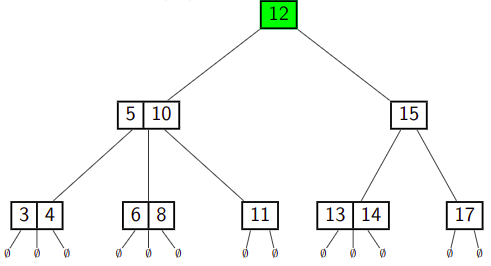
$(a,b)$ Tree

Properties

The $(2,4)$ Tree is a specific type of $(a,b)$ tree.

An $(a,b)$ tree satisfies:

1. Each node has at least $a$ subtrees, unless it is the root, which has at least $2$ subtrees.
2. Each node has at most $b$ subtrees.
3. If a node has $k$ subtrees, then it stores $k-1$ KVPs.
4. Empty subtrees are at the same level.
5. The keys in the node are between the keys in the corresponding subtrees.

Additionally, we set the rule that $a \geq b/2$, so operations for $(a,b)$ trees will work just like for $(2,4)$ trees, after re-defining underflow/overflow to consider above constraints.

Analysis

We now analyze the runtime for general $(a,b)$ trees.

Search

• We find the appropriate subtree for recursion in internal memory: $i\leftarrow \max\{i: k_i \leq k\}$. Searching sorted array takes $O(\log b)$ as we know the number of KVPs are bounded above by $b$.
• Since search takes $O(\log b)$ at each level, overall it takes $O(\log b \cdot h)$. Since we don't care about what's happening in internal memory, the number of block transfers is $O(h)$.

Insert

• The initial search takes $O(\log b \cdot h)$ with $O(h)$ block transfers.
• The splitting takes $O(h)$ worst case (we split at each level).
• Under the key assumption where each node fits into one block, the overall number of block transfers is again $O(h)$.

Height

Suppose we have an $(a,b)$ tree of height $h$. Note tha we don't count empty subtrees as a level. We want to build an $(a,b)$ tree with as few nodes as possible but still reach height $h$ to form a relationship between $n$, the number of KVPs, and $h$, the height of $(a,b)$ trees.

At layer 0, we have one node (root) and at least 1 KVPs (recall root is special).

At layer 1, we have at least two nodes (root is special where it can have two subtrees only), each node stores at least $(a-1)$ KVPs, so overall this layer has $2(a-1)$ KVPs.

At layer 2, we have at least $2a$ nodes (each node at layer $1$ has $a$ subtrees at least), each node stores at least $(a-1)$ KVPs, so overall this layer has $2a(a-1)$ KVPs.

At layer 2, we have at least $2a^2$ nodes (each node at layer 2 has $a$ subtrees at least), each node stores at least $(a-1)$ KVPs, so overall this layer has $2a^2(a-1)$ KVPs.

Continue this process, at layer $h$, we have at least $2a^{h-1}$ nodes, each node stores at least $(a-1)$ KVPs, so overall this layer has $2a^{h-1}(a-1)$ KVPs.

Sum up the number of KVPs, we get the number of KVPs given height $h$ is at least

Rearranging the equation, the height $h$ given $n$ of KVPs is at most

Since $\log_a n = \frac{\log_b n}{\log_b a}$ and the bottom is a constant, we get $h \in O(\log_b n)$.

Keep in mind that we have the assumption wehre $a \leq b$ and $a \geq b/2$ , because otherwise the insertion split wouldn't work.

Conclusion

Therefore, runtime for operations is $O(h) = O(\log_b n) = O(\log n)$ worst case! The number of block transfer is also $O(\log_b n)$.

$(2,4)$ Tree $\iff$ Red Black Tree

David: You are expected to know how the conversion works but not RBT insertion.

Note that we have another data structure with worst-case $O(\log n)$ performance besides AVL tree. We now show (using Red Black Tree) that $(2,4)$ trees perform better than AVL trees.

A brief introduction on Red Black Tree

• Properties:

  • Every node is red or black,
  • Subtrees of red nodes are empty or have black root,
  • Any empty subtree $T$ has the same black-depth, i.e., has the same number of black nodes on its path to the root.

• To convert a $(2,4)$ tree to a red-black tree: A $d$-node becomes a black node with $d-1$ red children.

• To convert a red-black-tree to $(2,4)$ tree: the black node and $0 \leq d \leq 2$ red children become a $(d+1)$-node.

In general, red-black-trees provide faster insertion and removal operations than AVL trees as fewer rotations are done due to relatively relaxed balancing.

B-Tree

We have seen the number of block transfers for an $(a,b)$ tree is $O(\log_b n)$. To minimize this, we want to maximize our base $b$. This is the central motivation for $B$-trees: we want to fit as many KVPs as possible into one block: a $B$-tree of order $m$ is a $\lfloor m/2\rfloor$-$m$-tree, where $m \approx \frac{B}{\text{size of a KVP}} \in \Theta(\log_Bn)$

B-Trees are basically useless in internal memory (no better than AVL or $(2,4)$ trees), but are great when used in external memory (e.g., database-related applications), as it minimizes the number of block transfers: recall each operation is done in $\Theta(h)$ block transfers, then $\Theta(h) = \Theta(\log_m n) = \Theta(\log_Bn)$ gives huge saving of block transfers as it minimizes height.

Two Futher Issues

1. What if we don't know $B$, the block size? Then we couldn't calculuate $m$ explicitly! Solution: we could use Cache Oblivious Trees (not tested).
2. What if the values are much bigger than the keys? For example, keys being Facebook ID and values being all the stuff our dearest Mark Zuckerberg has on us? Solution: Take a look at B⁺ trees.

B⁺-Tree

Motivation: Storage DS vs. Decision DS

There are two variants of tree-structures:

1. Storage-variant (Heap, BST): Every node stores a KVP.
2. Decision-variant (Trie, kd-Tree): All KVPs at leaves; internal nodes / edges store only decisions to guide search.

For storage-variant, there usually exists an equivalent decision variant. In internal memory this wastes space (usually twice as many nodes), but we could take advantage of this in external memory.

B⁺-Tree: The Decision-Variant of a B-Tree

B-tree of order 5:

B⁺-tree of order 5:

• All KVPs are in the leaves.
• Key at internal nodes holds minimum key from subtree to the right.
• Search/insert need some minor adjustments (no details).

Lemma on B^+-Tree Size

Claim. A B⁺ tree stores $< 2n$ keys, aassuming $a \geq 2$.

Proof. The bottom layer stores $n$ keys; one layer above stores $\leq n/a$ keys; the layer above stores $\leq n/a^2$ keys... Thus the total number of keys is

Why Do We Do This?

Assume keys are usually fairly small, while values potentially huge. Recall in B-tree, the order is chosen such that a node fits into a block. In a B⁺-tree, internal nodes can store many more keys than KVPs! Thus the height will be much smaller, so we need fewer block transfer.

Extendible Hashing

Motivation

We store integers in external memory. The regular hashing techniques we had before uses

• $O(1)$ expected runtime for insert and search,
• $O(1)$ expected number of block transfers.

But! This is amortized! Occationally you need to rehash/rebuild the entire data structure!

Rehashiing takes between $\Theta(n/B)$ and $\Theta(n)$ block transfers, which is too slow to our standard.

Tries of Blocks

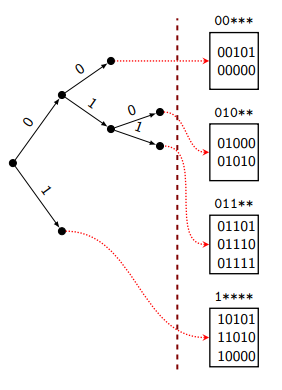
Assume we store integers (hash values) in $\{0, 1, \ldots, 2^L-1\}$. Note that we can control the outputs of hash values by choosing appropriate hash function(s).

• We interpret all integers as bitstrings of length $L$.
• Build a trie $D$ (directory) of integers in internal memory.
• The trie stops splitting when remaining items fit in one block.
• Each leaf of $D$ refers to the block in external memory that stores the items.

Operations

We define

• Global depth: how many steps do I need to walk from the root down to the deepest leaf.
• Local depth (of a block): how many steps do I need to walk from the root down to the given leaf.

In the example above, the global depth is $3$ and the top leaf has local depth $2$. The key observation is that the local depth for a block equals the number of mask of that block, i.e., the first few bits of the block that distinguishes itself, or the bits on the search path from root to that block (in the sense of trie search).

Search(k)

1. Compute $h(k)$ the hash value.
2. Convert $h(k)$ to a bitstring $x$.
3. Trace in trie of blocks to find $x$.
4. The leaf you reached contains a reference to the block with $x$ in it. Load that block and search for $x$.

Thus, the number of block transfers for search is $1$.

Insert(k)

1. Do $Search(k)$ as above and load the block that should have $k$.
2. If the block has space, add $k$ to it and return.
3. Otherwise, split the block and expand the trie until $k$ fits into the block.

Example: Insert(10110):

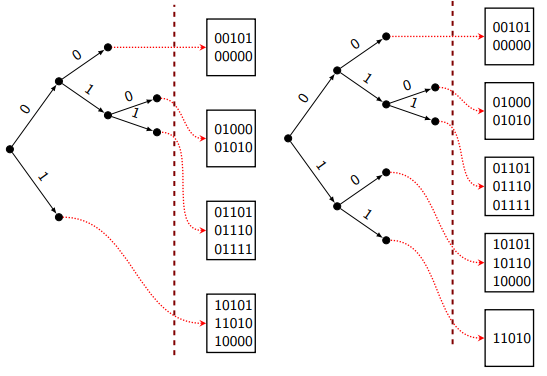
Pseudocode.

[On slides; TBC]

The number of block transfers could be bit but in practice usually 2 to 5:

• Load block once when searching.
• Create two new blocks when splitting.
• Write two new blocks back to external memory.

Discussion

1. We usually do $O(1)$ block transfer only and we never need a full rehash.
2. Note that we assumed the entire trie of directory fits into internal memory.
3. We may have empty or underfull blocks, so a bit of space wasted is inevitable.

To further save space, we could expand the trie so that all leaves have the global depth. Note that multiple leaves may point to the same block. Next, we store only the leaves in an array $D$ with size $2^{g}$ where $g$ is the global depth of the trie.

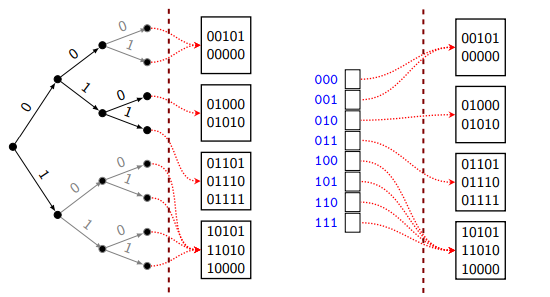
Try to think of doing insertion in a trie (instead of the optimized array thingy) when doing extendible hashing. This is probably easier for your brain.