Pattern Matching

CS240E: Data Structure and Data management (Enriched)

David Duan, 2019 Winter, Prof. Biedl

Motivation

Pattern Matching

Given a text $T = T[0 \cdots n-1]$ of length $n$ and a pattern $P = P[0 \cdots m-1]$ of length $m$ , we return the first $i$ such that $P[j] = T[i+j]$ for $0 \leq j \leq m-1$ , which is the index of the first occurrence of $P$ in $T$ , or FAIL, if $P$ does not occur in $T$ .

Definitions

A substring $T[i\cdots j]$ , $0 \leq i \leq j < n$ , is a string of length $j-i+1$ which consists of characters $T[i], \ldots, T[j]$ in order.
A prefix of $T$ is a substring $T[0 \cdots i]$ of $T$ for some $0 \leq i \leq n-1$ .
A suffix of $T$ is a substring $T[i \cdots n-1]$ of $T$ for some $0 \leq i \leq n-1$ .
A border of $T$ is a substring $r$ with $r = T[0\cdots b-1] = T[n-b \cdots n-1]$ where $b \in \{0, n-1\}$ . In other words, a border of $T$ is a substring that is both proper prefix and proper suffix of $x$ . We call its length $b$ the width of the border.
A guess or shift is a position $i$ such that $P$ might start at $T[i]$ . Note that the valid guesses initially are $0 \leq i \leq n-m$ .
A check of a guess is a single position $j$ with $0 \leq j < m$ where we compare $T[i+j]$ to $P[j]$ . Note that we must preform $m$ checks of a single correct guess, but may make fewer checks of an incorrect guess.

Brute-Force Algorithm

We check every possible guess.

\begin{align*} &BruteforcePM(T[0 \cdots n-1], P[0 \cdots m-1]) \\ &T: \text{Text, string of length $n$.} \\ &P: \text{Pattern, string of length $m$.}\\ \\ &1. \quad \text{for $i \leftarrow 0$ to $n - m$ do} \\ &2. \qquad \text{if $strcmp(T[i \cdots i+m-1], P) = 0$} \\ &3. \qquad \quad \text{return $i$ } \\ &4. \quad \text{return $-1$} & \text{Pattern DNE, FAIL} \end{align*}

The worst case performance is $\Theta((n-m+1)m)$ , as there are $n-m+1$ valid guesses and checking for each guess (string comparison) takes $\Theta(m)$ time.

The runtime for brute-force algorithm is $\Theta(mn)$ , which is quadratic if $m$ is large!

Improvement

To improve the performance, we can break the problem into two parts:

Preprocessing: we build data structures or extract information that makes query easier, which may take a long time,
Query: we carry out the original task, which should be very fast as we have already paid the price during the first stage.

The Range Query problem in our previous module can be seen an example of prepocessing.

For Pattern Matching, we can either do preprocessing on the pattern $P$ , where we eliminate guesses based on completed matches and mistakes, or on text $T$ , where we create a data structure to make finding matches faster.

Karp-Rabin Algorithm

Key Idea We use hashing to eliminate guesses.

$h(k_1) \ne h(k_2) \implies k_1 \ne k_2$ , i.e., there is no need for $strcmp$ if hash values differ.
$h([x_0\cdots x_4]) = (x_0x_1x_2x_3x_4)_{10} \mod M$ where $M$ is a prime.

Karp-Rabin Fingerprint Algorithm (Naive)

Strategy

The initial hashes are called fingerprints. We compute the fingerprint/hash value (using the ordinary flatten-then-modular approach) for each substring of length $m$ in $T$ . If this fingerprint equals the fingerprint for the pattern, we $strcmp$ them to check if it really is a match; otherwise, we discard the current guess.

Pseudocode

\begin{array}{ll} &KarpRabinNaive(T, P) \\ &1. \quad h_P \leftarrow h(P[0\cdots m-1]) &\text{Compute hash value for the pattern}\\ &2. \quad \text{for $i \leftarrow 0$ to $n-m$} \\ &3. \qquad h_T \leftarrow h(T[i\cdots i+m-1]) &\text{Compute hash value for a guess} \\ &4. \qquad\quad \text{if $h_T = h_P$} \\ &5. \qquad\qquad \text{if $strcmp(T[i\cdots i+m-1], P)=0$} \\ &6. \qquad\qquad\quad \text{return $i$} \\ &7. \quad \text{return $-1$} & \text{Pattern DNE, FAIL} \end{array}

Correctness

We will never miss a match, as $h(T[i\cdots i+m-1]) \ne h(P) \implies T[i\cdots i+m-1] \ne P$ .

Complexity

The overall runtime is still $\Theta(mn)$ worst case as computation (line $3$ ) depends on $m$ characters.

We didn't really improve anything!

Karp-Rabin Fingerprint Algorithm (Rolling Hash)

Strategy

Suppose in a previous iteration, we have computed $h(41592) = 76$ , and now we want $h(15926) = 15926 \mod 97$ . Observe $15926 = (41592 - 4 \cdot 10000) \cdot 10 + 6$ . Thus:

\begin{align*} 15926 \mod 97 &= \Big((\overbrace{41592 \mod 97}^\text{previous hash value} - 4 \cdot \overbrace{10000 \mod 97}^\text{we can precompute this}) \cdot 10 + 6\Big) \mod 97 \\ &= ((h_p - 4 \cdot s) \cdot 10 + 6) \mod 97& \in O(1)! \end{align*}

Given the hash value of the previous guess, we can compute the hash value of the next guess in constant time!

Pseudocode

\begin{array}{ll} &KarpRabinRollingHash(T, P) \\ &1. \quad h_P \leftarrow h(P[0\cdots m-1]) &\text{Compute hash value for the pattern}\\ &2. \quad p \leftarrow \text{suitable prime number for hashing} \\ &3. \quad s \leftarrow 10^{m-1}\mod p \\ &4. \quad h_T \leftarrow h(T[i\cdots i+m-1]) &\text{Compute hash value for the first guess} \\ &5. \quad \text{for $i \leftarrow 0$ to $n-m$} \\ &6. \qquad\quad \text{if $i > 0$} &\text{Compute hash value for the next guess}\\ &7. \qquad\qquad h_T \leftarrow ((h_T - T[i] \cdot s) \cdot 10 + T[i+m]) \mod p\\ &8. \qquad\quad \text{if $h_T = h_P$} &\text{If fingerprints match, we do $strcmp$}\\ &9. \qquad\qquad \text{if $strcmp(T[i\cdots i+m-1], P)=0$} \\ &10. \qquad\qquad\;\; \text{return $i$} \\ &11. \;\; \text{return $-1$} & \text{Pattern DNE, FAIL} \end{array}

Correctness

Correctness for rolling hash comes from modular arithmetic. The rest are identical to before.

Complexity

Worst case is still $\Theta(mn)$ but this is very unlikely. The expected time is $O(m+n)$ , where we spend $O(m)$ doing the initial computations and $strcmp$ and during each guess (roughly $O(n)$ of them) we perform constant operations.

This is easy and already faster than brute-force, but we can do even better!

Boyer-Moore Algorithm

Key Idea We compare the characters of the pattern and the substring from text from right to left, skipping the unnecessary comparisons by using the good-suffix and bad-character heuristics.

We compare the end characters of the pattern with the text. If they do not match, then the pattern can be moved on further. If the characters do not match in the end, there is no need to do further comparisons. In addition, we can also see what portion of the pattern has matched (matched suffix), so we could utilize this information and align the text and pattern by skipping any unnecessary comparisons. At the time of a mismatch, each heuristic suggests possible shifts, and the BM algorithm shifts the pattern by considering the maximum shift possible due to two heuristics.

Notation In the following examples, let ! denote the mismatched character and # denote the starting position of $P$ after our shift $P$ .

Bad Character Heuristic

This heuristic is based on the mismatched character.

If there is a mismatch between the character of the pattern and the text, then we check if the mismatched character of the text occurs in the pattern or not. If this mismatched character does not appear in the pattern, then the pattern will be shifted next to this character; if the character appears somewhere in the pattern, we shift the pattern to align with the occurrence of that character with the bad character of the text string.

Example I

The mismatched character is at $i = 5$ , where we see $b \ne c$ . Since $b \notin P$ , we can shift $P$ to $i + 1 = 6$ , i.e., our next guess is $T[6\cdots 11]$ , since substrings $T[0\cdots5], T[1\cdots 6], \ldots, T[5\cdots 10]$ all contain $b$ but $P$ does not. This saves us many unnecessary comparisons.


                                          #  
            i     0   1   2   3   4   5   6   7   8   9   0   1
                =====================================================
            T   | a | c | a | c | a | b | a | c | a | b | a | b | a |
                =====================================================
            P   | a | c | a | c | a | c |
                =====================================================
                                        | a | c | a | c | a | c |
                =====================================================
                                      ✗

Example II

We have a matched suffix $ac$ and mismatched character $d$ at $i = 3$ . Since $d \notin P$ , we shift $P$ to $i + 1 = 4$ .


xxxxxxxxxx
                                  #
            i     0   1   2   3   4   5   6   7   8   9   0   1
                =====================================================
            T   | a | c | a | d | a | c | a | c | a | b | a | b | a |
                =====================================================
            P   | a | c | a | c | a | c |
                =====================================================
                                | a | c | a | c | a | c |
                =====================================================
                              ✗  ✓  ✓

Example III

We have a matched suffix $ac$ and mismatched character $d$ at $i = 3$ . This time $d \in P$ and the only occurrence of $d$ is at $j = 1$ . Thus, we shift $P$ to $2$ to align $T[i]$ and $P[j]$ .


xxxxxxxxxx
                          #   !
            i     0   1   2   3   4   5   6   7   8   9   0   1
                =====================================================
            T   | a | c | a | d | a | c | a | c | a | b | a | b | a |
                =====================================================
            P   | a | d | a | c | a | c |
                =====================================================
                        | a | d | a | c | a | c |        
                =====================================================
                              ✗  ✓  ✓

Example IV

We have a matched suffix $cc$ and a mismatched character $a$ at $i = 3$ . This time however, there are two occurrences of $a$ in $P$ , each at $j = 0$ and $j = 2$ . We always shift the minimal amount to avoid missing any possible match. In this case, we prefer $P_1$ , because we only shift $1$ character, where $P_2$ shifts $3$ (and missed the matched string at $T[1\cdots 6]$ ! I came up with this example to show the importance of align the bad character to its last occurrence in the pattern).


xxxxxxxxxx
                      #       !     
            i     0   1   2   3   4   5   6   7   8   9   0   1
                =====================================================
            T   | a | a | c | a | c | c | c | c | a | b | a | b | a |
                =====================================================
            P   | a | c | a | c | c | c |
                =====================================================
            P1      | a | c | a | c | c | c |  
                =====================================================
            P2              | a | c | a | c | c | c |
                =====================================================
                              ✗  ✓  ✓

Last Occurrence Function

In Example IV, we saw the importance of aligning the bad character to its last occurrence in the pattern. Therefore, we need a last-occurrence function $L:\Sigma \to \N_0$ , where

L(c) = \begin{cases} \max\{i:P[i] = c\} & c \in P \\[10pt] -1 & c \notin P \end{cases}

For Example IV, $L(a) = 2$ , $L(c) = 5$ , and $L(x) = -1$ for all $x \in \Sigma \setminus \{a,c\}$ . When we see the mismatched $a$ at $i = 3$ , check $L(a) = 2$ and shift $3 - 2 = 1$ character.

Boyer-Moore Pseudocode (Bad Character Heuristic)

\begin{array}{ll} &BoyerMooreBCH(T,P) \\ &1. \quad L \leftarrow \text{Last occurrence array computed from $P$} \\ &2. \quad i \leftarrow 0 &\text{Current guess} \\ &3. \quad \text{while $i \leq n - m$} &\text{$i > n-m$ means no more valid guesses} \\ &4. \qquad \text{for $(j \leftarrow m-1, j \geq 0, j--)$} &\text{Comparing from right to left} \\ &5. \qquad \quad \text{if $T[i+j] \ne P[j]$ break} &\text{Found a mismatch}\\ &6. \qquad \text{if $j = -1$ return $i$} &\text{Finished comparing, everything matched}\\ &7. \qquad \text{else $i \leftarrow i + \max\{1, j-L[T[i+j]]\}$} &\text{See remark}\\ &8. \quad \text{return $-1$} & \text{Pattern DNE, FAIL} \end{array}

Remark. Sometimes $j - L[T[i+j]]$ produces a negative value:


xxxxxxxxxx
            i     0   1   2   3   4   5   6   7   8   9   0   1
                =====================================================
            T   | a | b | a | a | b | a | c | c | a | b | a | b | a |
                =====================================================
            P   | c | a | b | a | b
                =====================================================
                          ✗  ✓  ✓

If we were to align $T[2]$ with the last occurrence of $a$ in $P$ , we would need to shift $-1$ . To avoid negative shifting, we take $i + \max\{i, j-L[T[i+j]]\}$ , which guarantees that $i$ is incremented by at least $1$ . This also motivates the Good Suffix heuristic as we could do better than only shifting $1$ in the worst case.

Good Suffix Heuristic

This heuristic is based on the matched suffix.

We shift the pattern to the right in such a way that the matched suffix subpattern is aligned with another occurrence of the same suffix in the pattern.

For this heuristic, an array $S$ is used. Each entry contains the shift distance of the pattern if a mismatched at position $i-1$ occurs, i.e., if the suffix of the pattern starting at position $i$ has matched. In order to determine the shift distance, two cases have to be considered.

The matching suffix occurs somewhere else in the pattern.
The suffix of the matching suffix occurs as a prefix of the pattern.

Example I: Align Suffix


xxxxxxxxxx
                             !,#
            i     0   1   2   3   4   5   6   7   8   9   0   1
                =====================================================
            T   | l | m | n | n | p | a | ...
                =====================================================
            P   | s | p | a | a | p | a |
                =====================================================
                            | s | p | a | a | p | a |      
                =====================================================
                              ✗  ✓  ✓

We matched suffix $pa$ and found a mismatch at $3$ , where $P[3] = a$ but $T[3] = n$ . Therefore, we want to shift forward. The intuition is that, after shifting, two characters aligned with $T[4]$ and $T[5]$ must be $pa$ , otherwise it is guaranteed to fail. Since $pa$ occurs in $P$ at $1$ (recall this is the index where the substring $pa$ starts), we align $P[1]$ with $T[4]$ for our next guess.

Example II: Minimal Shifting


xxxxxxxxxx
                              #           !
            i     0   1   2   3   4   5   6   7   8   9   0   1
                =====================================================
            T   | n | p | a | l | m | n | n | p | a | a | p | a |
                =====================================================
            P   | n | p | a | n | p | a | a | p | a |
                =====================================================
                            | n | p | a | n | p | a | a | p | a |
                =====================================================
                                          ✗  ✓  ✓

In this example, there are two occurrences of $pa$ in $P$ . We always prefer the minimal amount of shifting to avoid missing possible matches.

Example III: Character Before Suffix


xxxxxxxxxx
                                         #,!
            i     0   1   2   3   4   5   6   7   8   9   0   1
                =====================================================
            T   | a | b | c | d | e | f | a | a | a |
                =====================================================
            P   | n | a | a | p | a | a | p | a | a |
                =====================================================
            P1                          | n | a | a | p | a | a | ...
                =====================================================
            P2              | n | a | a | p | a | a | p | a | a |
                =====================================================
                                          ✗  ✓  ✓

In this example, we matched suffix $aa$ and the mismatch occurs at $i=6$ , which tells us that $p$ in front of the matched suffix $aa$ doesn't work. Therefore, shifting to make $P[3]$ align with $T[6]$ will make us compare $P_2[4] = p$ with $T[6] = a$ , which we already know from the first iteration that $paa$ is bad. Thus, we shift to make $P[0]$ align with $T[6]$ to avoid unnecessary comparisons.

Example IV: Bad Character & Good Suffix


xxxxxxxxxx
                                         #,!
            i     0   1   2   3   4   5   6   7   8   9   0   1
                =====================================================
            T   | a | b | c | d | e | f | x | a | a |
                =====================================================
            P   | n | a | a | p | a | a | p | a | a |
                =====================================================
                                            | n | a | a | p | a | a | ...
                =====================================================
                                          ✗  ✓  ✓

If we were only to use good-suffix heuristic, we would shift the same way as in Example III. However, the bad-character heuristic tells us $x$ does not occur in $P$ at all, so we shift $P$ to one character after $x$ . The previous three examples are designed in the way that we can ignore the bad-character heuristic.

Example V: Suffix of Suffix Matches Prefix of Pattern


xxxxxxxxxx
                              !               #
            i     0   1   2   3   4   5   6   7   8   9   0   1
                =====================================================
            T   | a | b | c | a | a | b | b | a | b | b | a |
                =====================================================
            P   | a | c | b | b | a | b | b | a |
                =====================================================
            P1              | a | c | b | b | a | b | b | a |
                =====================================================
            P2                              | a | c | b | b | ...
                =====================================================
                             ✗

The matched suffix is $abba$ , but $abab$ is not occurred elsewhere in our pattern $P$ . We then search for partial suffix, or suffix of this suffix (which is still a suffix of $P$ ), see if any part of it is a prefix for $P$ . Note that we only accept when a partial suffix is a prefix of $P$ ; anywhere else the partial suffix occurs in $P$ are not accepted. Consider the above example. We know $abba$ is not occurred elsewhere in $P$ , so we start searching if a partial suffix is a prefix of $P$ . Although $bba$ does occur, we know the character preceding $bba$ is a mismatch (otherwise, $abba$ would occur), so we don't accept this occurrence of $bba$ in the middle of $P$ . Thus, $P_1$ is wrong. The correct shift is $P_2$ , where we see $a$ is both a suffix and a prefix of $P$ .

Example VI: Together


xxxxxxxxxx
                              !               #
            i     0   1   2   3   4   5   6   7   8   9   0   1
                =====================================================
            T   | c | h | u | a | c | h | u | p | i | k | a | p | ...
                =====================================================
            P   | p | i | k | a | c | h | u |
                =====================================================
            P1                              | p | i | k | a | c | ...
                =====================================================
                         ✗

By bad-character, we would shift $1$ forward (recall the argument " $1$ " to the $\max$ function in the previous $BoyerMooreBCH$ algorithm). By good-suffix, since there is no suffix of $achu$ that is also a prefix of $pikachu$ , we shift the entire thing past the current location, because we know non-of the substrings $T[1\cdots 7], \cdots, T[6 \cdots 12]$ would work.

Suffix Skip Array

We can precompute the suffix skip array of amount to shift, where

Then, we can update guess by $i \leftarrow i + (m - i - S[j])$ . This is computable in $\Theta(m)$ time (similar to KMP failure function, see below).

Conclusion

BM works well in practice, even bad-character heuristic alone is often good enough.
Preprocessing takes $\Theta(m+|\Sigma|)$ : $\Theta(|\Sigma|)$ for last-occurrences and $\Theta(m)$ for suffix-skip.
Search takes $\Theta(n)$ time (often better in practice).
Auxiliary space $\Theta(m+|\Sigma|)$ : $\Theta(|\Sigma|)$ for last-occurrences and $\Theta(m)$ for suffix-skip.

Knuth-Morris-Pratt Algorithm

Motivation

Recall from CS241 (yikes), we could match strings using DFAs. We could embrace the idea of using states to represent our matching progres. In addition, we have a new type of transition $\times$ (failure):

Use this transition only if no other fits.
Does NOT consume a character (like an $\varepsilon$ -transition).

With these rules, computations of the automaton are deterministic (but not formally a valid DFA).

How the Automaton Works

Recall if we are at state $j$ , then we have the first $j$ characters matched at this moment.

The following automaton helps us match the pattern $ababaca$ :

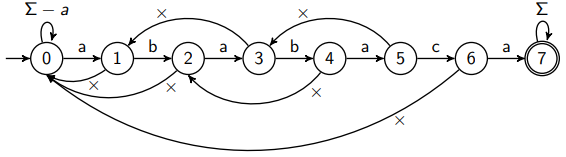
The normal transitions and states are intuitive (same as in CS241). To understand the failure transitions, consider what happens when we feed it the following inputs:

$ababaca$ : Trivial; we get to the accepted state 7.
$abcX$ : $ab$ matched so we get to state 2. However, the next character is a mismatch (we see this by comparing the next character in the input string, i.e., $c$ , with the character for the valid transition at the current state, i.e., $a$ ), so we follow the failure arc from state 2, which sends us back to state 0. We then compare the next character $c$ with the character for a valid transition character $a$ , which is a mismatch. Thus, we follow the loop and stay in state 0. Intuitively, this means that we need to start from the beginning when we match $X$ .
$aaX$ : $a$ matched so we get to state 1. However, the next one is a mismatch, so we don't consume anything and follow the failure arc back to 0. Since next character is $a$ and the character for valid transition is also $a$ , we can go to state 1. Intuitively, this means that when we start matching $X$ , we have already matched an $a$ .
$ababeX$ : The first four letters matched, so we are at state 4. Next character is a mismatch, so we follow the failure arc of state 4 to go back to state 2. The transition fails at state 2 again, so we follow the failure arc back to 0. Since $e \ne a$ , we follow the loop and stay at state 0. This means the same as $abcX$ .

Following the failure arc is equivalent to shifting our pattern forward.

Failure Array

We can compute and store these failure arcs using an array $F[0\cdots m-1]$ , where the failure arc from state $j$ leads to $F[j-1]$ . The indices differ by $1$ because we don't need to store the failure arc for state $0$ , as it has a loop if the character for valid transition doesn't match. Thus, $F[0]$ stores the destination of failure arc originated from state 1 (which is always 0) and $F[j]$ stores the destination of failure arc orginated from state $j+1$ .

Brute Force

Since we are basically trying to find the longest proper prefix of $P$ that is also a proper suffix of $P$ , we could do the following in $O(m^3)$ time (suppose $P = ababaca$ ):

We consider $P[1\cdots j]$ because we want proper suffixes of $P$ . $F[j]$ is the length of the longest prefix of $P$ that is a suffix of $P[i \cdots j]$ .

Example: An Intuitive Way to Compute Failure Array

$P[0 \cdots i-1]$	$a$	$ab$	$aba$	$abab$	$ababa$	$ababac$
New Character	$a$
Longest Valid Proper Prefix & Suffix of $P[0 \cdots i-1]$
Current State and Valid Character Transition

Let our starting state be $0$ and process the first character $p = P[0] = a$ . There is no valid proper prefix of $p$ that is also a proper suffix, so the substring is $\varepsilon$ . Intuitively, if we fail transition for next character, we would go back to state $0$ .

$P[0 \cdots i-1]$	$a$	$ab$
New Character	$a$	$b$
Longest Valid Proper Prefix & Suffix of $P[0 \cdots i-1]$	$\varepsilon$
Current State and Valid Character Transition	$0, a$

We are at state $0$ and the new character is $b$ . The valid transition character from current state (we look at the previous column!) does not match our new character, so we can't extend the substring. Thus, we stay at $0$ with the substring being $\varepsilon$ .

$P[0 \cdots i-1]$	$a$	$ab$	$aba$
New Character	$a$	$b$	$a$
Longest Valid Proper Prefix & Suffix of $P[0 \cdots i-1]$	$\varepsilon$	$\varepsilon$
Current State and Valid Character Transition	$0, a$	$0,a$

We are still at state $0$ and the new character is $a$ . This time, the valid transition character (again, last column) matches our new character so we know we can extend our substring. In other words, previous substring plus new character, i.e., $\varepsilon + a = a$ is our current longest valid proper prefix and suffix after seeing $aba$ . We increment our state, so that the destination of the failure arc from state $3$ is state $1$ .

$P[0 \cdots i-1]$	$a$	$ab$	$aba$	$abab$
New Character	$a$	$b$	$a$	$b$
Longest Valid Proper Prefix & Suffix of $P[0 \cdots i-1]$	$\varepsilon$	$\varepsilon$	$a$
Current State and Valid Character Transition	$0, a$	$0,a$	$1,b$

We are at state $1$ and the new character is $b$ , which matches the valid transistion character at current state. We add $b$ to current substring and increment our state. Note that at any time, the second row could serve as a sanity check to see if your algorithm is wrong.

$P[0 \cdots i-1]$	$a$	$ab$	$aba$	$abab$	$ababa$
New Character	$a$	$b$	$a$	$b$	$a$
Longest Valid Proper Prefix & Suffix of $P[0 \cdots i-1]$	$\varepsilon$	$\varepsilon$	$a$	$ab$
Current State and Valid Character Transition	$0, a$	$0,a$	$1,b$	$2,a$

Following the same logic, characters match so we extend the substring and increment state.

$P[0 \cdots i-1]$	$a$	$ab$	$aba$	$abab$	$ababa$	$ababac$
New Character	$a$	$b$	$a$	$b$	$a$	$c$
Longest Valid Proper Prefix & Suffix of $P[0 \cdots i-1]$	$\varepsilon$	$\varepsilon$	$a$	$ab$	$aba$	$\varepsilon$
Current State and Valid Character Transition	$0, a$	$0,a$	$1,b$	$2,a$	$3,b$	$0,a$

This time, $c != b$ , so we follow the failure arc at state $3$ to go back to $1$ ; $c != b$ (comparison at state $1$ ) so we follow the failure arc at state $1$ to go back to $0$ . At this point, the substring is empty and our stay at $0$ . Note that we don't need to compute for the last state, because if we got there then our text is accepted; we can happily write $\square$ and move on.

Pseudocode

\begin{array}{ll} &failureArray(P) \\ &P: \text{Pattern, string of length $m$} \\ &1. \quad F[0] \leftarrow 0 &\text{At state $1$, we always go back to $0$}\\ &2. \quad i \leftarrow 1 &\text{Current character of $P$ to compute the failure arc} \\ &3. \quad j \leftarrow 0 & \text{Current state that we are in; $P[j]$ denotes the transition character}\\ &4. \quad \text{while $i < m$ do} &\text{Compute for each character (no need for the first one)}\\ &5. \qquad \text{if $P[i] = P[j]$} &\text{If current character equals the valid transition character}\\ &6. \qquad \quad j \leftarrow j + 1 &\text{We can build a longer substring that is both prefix and suffix} \\ &7. \qquad \quad F[i] \leftarrow j &\text{Where our failure arc from current state should go to}\\ &8. \qquad \quad i \leftarrow i + 1 &\text{We process the next character} \\ &9. \qquad \text{else if $j > 0$} &\text{If next character is a mismatch} \\ &10. \qquad \;\; j \leftarrow F[j-1] &\text{We follow the failure arc at current state}\\ &11. \quad \;\; \text{else} &\text{There is no more failure arcs to follow, i.e., we are at $j = 0$}\\ &12. \qquad \;\; F[i] \leftarrow 0 &\text{Set current failure state to be state $0$} \\ &13. \qquad \;\; i \leftarrow i + 1 &\text{We process the next character} \end{array}

The loop invariant is that, $P[0\cdots j]$ is the longest valid prefix and valid suffix of pattern $P$ after we have seen $P[0 \cdots i-1]$ .

Claim Failure array takes $\Theta(m)$ to compute.

Proof. Consider how $2i - j$ changes in each iteration of the while loop:

$i$ and $j$ both increase by $1$ $\implies 2i-j$ increases.
$j$ decreases as $F[j-1] < j \implies 2i-j$ increases.
$i$ increases $\implies 2i-j$ increases.

Initially $2i -j \geq 0$ and at the end $2i - j\leq 2m$ . Thus, the while loop runs less than $2m$ iterations $\implies \Theta(m)$ runtime. $\square$

KMP Algorithm

\begin{array}{ll} &KMP(T, P) \\ &1. \quad F \leftarrow failureArray(P) &\text{First compute the failure array, $\Theta(m)$}\\ &2. \quad i \leftarrow 0 &\text{Current character of $T$ to parse}\\ &3. \quad j \leftarrow 0 &\text{Current state that we are in} \\ &4. \quad \text{while $i < n$ do } &\text{While there's remaining text}\\ &5. \qquad \text{if $P[j] = T[i]$} & \text{If character matches} \\ &6. \qquad \quad \text{if $j = m - 1$} & \text{If this is the last character of the patterm}\\ &7. \qquad \qquad \text{return "found at guess $i - m + 1$"} &\text{We are good}\\ &8. \qquad \quad \text{else} &\text{We have more characters to parse/match} \\ &9. \qquad\qquad i \leftarrow i + 1, \quad j \leftarrow j + 1 &\text{Increment both ptrs}\\ &10. \quad \;\; \text{else} & \text{If current character does not match} \\ &11. \qquad \;\; \text{if $j > 0$} & \text{If we are not at state $0$} \\ &12. \qquad \quad \;\; j \leftarrow F[j-1] & \text{Follow the failure arc (We dont consume $F[i]$!)} \\ &13. \qquad \;\; \text{else} & \text{If we are at state $0$} \\ &14. \qquad \quad \;\; i \leftarrow i + 1 & \text{Follow the failure arc} \\ &15. \;\; \text{return $-1$} & \text{Pattern DNE, FAIL} \end{array}

Claim The runtime overall is $\Theta(n+m)$ .

Proof. Failure array can be computed in $\Theta(m)$ time. The same analysis shows that the while loop in the main function runs less than $2n$ iterations as $2i - j \leq 2n$ . Thus, the overall runtime is $\Theta(n+m)$ . $\square$

Suffix Trees

Motivation

KR, BM, and KMP all try to speed up pattern matching by preprocessing $P$ . We can also preprocess the text $T$ , especially when we want to search for many patterns $P$ within the same fixed text $T$ .

Observe that $P$ is a substring of $T$ iff $P$ is a prefix of some suffix of $T$ . Thus, we could store all suffixes of $T$ in a trie and do a trie-search for pattern matching.

Suffix Tree

To save space, we use a compressed trie and store suffixes implicitly via indices into $T$ .
Each internal node stores a reference to a leaf.
We could build a suffix tree in $O(n)$ time, but this is too complicated and we are not studying it in this course.
Note that, if $T$ has $n$ characters, it will have $n+1$ suffixes (the additional one being $\varepsilon$ ). Thus, the suffix tree has size $O(n)$ .

Pattern Matching

Recall in an uncompressed trie of suffixes, we parse $P$ until "no such child" or "found as perfix". Similarly in a suffix tree, we parse $P$ until

No such child, return $-1$ .
Reached a leaf, check existence,
Run out of characters, check existence.

Example

Consider the following suffix tree for $T = bananaban\$$ :

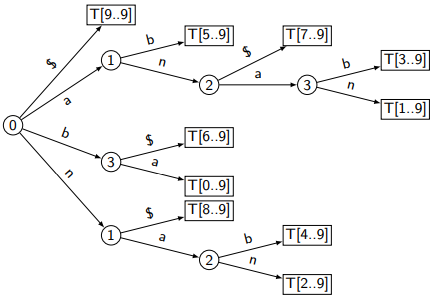
$P = ann$ : At node $2$ , we see there is no edge/transition for $n$ , so "no such child" and return $-1$ .

$P=ana$ : We ran out of characters in $P$ and stop at state $3$ . Since the node stores a reference to the leaf which stores the longest suffix, i.e., $T[1 \cdots 9]$ , we check if $P$ is in $T[1 \cdots 9]$ . Note that the lower bound $i = 1$ tells us that, if $P$ exists, it must start at $T[1]$ . We see $P = ana = T[1\cdots 3]$ , thus we found a match.

$P=briar$ : We parse $P[0]$ and follow the path $0\to 3$ , then parse $P[3]$ to follow that path $3 \to T[0\cdots 9]$ . We are at a leaf. We know $P[0] = T[0]$ and $P[3] = T[3]$ , but we don't know about $P[1], P[2]$ , or the rest of $P$ , since the "compression" skipped the comparisons for those characters. We do $strcmp(P, T[0\cdots 5])$ and found they are different. Hence no match.

Check Existence

From the above example, we see that even if we have exhausted characters in $P$ or reached a leaf in $T$ , we still can't guarantee that $P$ exists in $T$ without further $strcmp$ .

Recall we store suffixes implicitly via indices into $T$ . To check if $P$ is in $T$ , we do $strcmp(P, T[i \cdots i+m-1])$ , where $i$ tells us "if $P$ exists, it starts at $i$ ". As a side note, we want to make sure $i + m - 1 \leq n -1$ , i.e., no overflow (for example, we could do early stop when overflow is detected).

Pseudocode

\newcommand{\T}{\mathcal T} \begin{array}{ll} &SuffixTreePM(T[0\cdots n-1], P[0\cdots m-1], \T) \\ &T:\text{text},\quad P:\text{pattern},\quad \T:\text{suffix tree of $T$}\\ &1. \quad v \leftarrow \T.root &\text{Start parsing at the root} \\ &2. \quad while \text{ True}: &\text{Stop conditions are inside the body}\\ &3. \qquad w \leftarrow \text{child of $v$ corresponding to $P[v.index]$} & \text{$v.index$: relevant character} \\ &4. \qquad \text{if there is no such child, return $-1$} &\text{No such child case: FAILURE}\\ &5. \qquad \text{if $w$ is a leaf or $w.index \geq m$} &\text{Reached leaf or exhausted $P$}\\ &6. \qquad \quad \ell \leftarrow \text{leaf in subtree of $w$} &\text{Go to the referenced leaf} \\ &7. \qquad \quad \text{if $(\ell.start +m-1 < n)$} &\text{Make sure no out-of-bounds}\\ &8. \qquad \qquad \text{if $(strcmp(T[\ell.start \cdots \ell.start+m-1], P) = 0)$} &\text{Check existence} \\ &9. \qquad \qquad \quad \text{return "Matched at guess $\ell.start$"} &\text{SUCCESS} \\ &10. \qquad \;\; \text{else return FAIL} &\text{FAILURE}\\ &11. \quad \;\; v \leftarrow w &\text{Go to the next character} \end{array}

$v.index$ indicates which character in $P$ are we concerning. In the example above, suppose $P = ban$ . In the beginning, $v.index = 0$ tells us we need to follow the transitions from root based on $P[0]$ . Thus, we follow branch labeled $b$ and arrive at the node labeled $3$ (our $w$ ). However, $w.index \geq m = 3$ , telling us we have exhausted $P$ . We then do strcmp to check the existence of $ban$ in $T[0 \cdots 9]$ , which is the longest leaf pointed to by $w$ .

Analysis

Preprocessing takes $O(n)$ (blackbox algorithm).
Search time takes $O(m)$ as we are walking down the trie and consume one character from $P$ each time; the loop stops after at most $m$ iterations.
We need $O(n)$ extra space as the suffix tree has size $O(n)$ .

Suffix Array

Motivation

We want a pattern matching algorithm that is almost as fast as suffix trees but requires much less space and is easier to work with.

We sort all suffixes of text $T$ and store the sorted indices in an array $A^s$ , i.e., $A^s[i] = j$ iff suffix $T[j, \ldots, n-1]$ is the $i$ -th smallest suffix. For pattern matching, we need to find $P$ among suffixes that are in sorted order. With binary search, we could achieve this in $\Theta(\log n)$ comparison. However, notice each comparison is a strcmp of $P$ and $T[i, i+m-1]$ , which takes $O(m)$ time. Thus, runtime is $O(m \log n)$ (compared to $O(m)$ for suffix trees). This is the price we pay for space efficiency.

Pattern Matching in Suffix Arrays

Consider the following example. Given $T = [t, a, r, a, n, t, u, l, a]$ , we sort all its suffixes:

\begin{array}{llmrr} i & \text{$i$-th suffix} && i & \text{$i$-th suffix} \\ 0 & tarantula & & 8 & a \\ 1 & arantula & & 3 & antula\\ 2 & rantula & & 1 & arantula\\ 3 & antula & \implies & 7 & la \\ 4 & ntula && 4 & ntula \\ 5 & tula && 2 & rantula\\ 6 & ula && 0 &tarantula \\ 7 & la && 5 & tula\\ 8 & a && 6 & ula \end{array}

The suffix array $A^s$ here is $[8, 3, 1, 7, 4, 2, 0, 5, 6]$ . If we are given this, we could do a simple binary search to determine if $P$ exists in $T$ .

\begin{array}{ll} &SuffixArraySearch(A^s, P) \\ & A^s[0 \cdots n-1]: \text{Suffix array of $T$} \\ &P[0 \cdots m-1]: \text{Pattern} \\ &1. \quad \ell \leftarrow 0; r \leftarrow n-1 & \text{Initialize flags for binary search} \\ &2. \quad \text{while $(\ell \leq r)$} &\text{Binary search} \\ &3. \qquad m \leftarrow \lfloor \frac{\ell + r}{2} \rfloor &\text{Middle flag}\\ &4. \qquad j \leftarrow A^s[m] & \text{Current suffix to be compared: $T[j\cdots n-1]$} \\ &5. \qquad c \leftarrow strcmp(T[j \cdots j + m - 1], P) & \text{String comparison} \\ &6. \qquad \text{if $(c=-1)$}: \ell = m + 1 & \text{Current suffix too small, move right}\\ &7. \qquad \text{else if $(c=1)$}: r = m - 1 & \text{Current suffix too large, move left} \\ &8. \qquad \text{else: return "Found at $T[j \cdots j + m - 1]$} & \text{Success} \\ &9. \qquad \text{return "Not found"} & \text{Failure:DNE} \end{array}

For example, if we were to search if $ant$ exists in $T = tarantula$ , the above algorithm runs as follows:

$\ell \leftarrow 0$ , $r = 8$ . ( $|T| = 9 \implies r = n - 1 = 8$ .)
First iteration: $m = 4$ , $A^s[4] = ntula$ . $strcmp(ntu, ant)$ returns $1$ as $ntu > ant$ . $r \leftarrow 3$ .
Second iteration: $m = 1$ , $A^s[1] = antula$ . $strcmp(ant, ant)$ returns $0$ . Success.

Build Suffix Array

How do we efficiently build the suffix array? Suppose we have $T = bananaban$ .

Given the unsorted suffix array (left), we countSort by first letter. Recall it is stable:

\begin{array}{||l|l|m|r|r||} i & \text{$i$-th suffix} && i & \text{$i$-th suffix} \\ \hline 0 & bananaban & & 1 & ananaban \\ 1 & ananaban & & 3 & anaban\\ 2 & nanaban & & 5 & aban\\ 3 & anaban & \implies & 7 & an \\ 4 & naban && 0 & bananaban \\ 5 & aban && 6 & ban\\ 6 & ban && 2 & nanaban \\ 7 & ab && 4 & naban \\ 8 & n && 8 & n \end{array}

Next, we partition the (partially) sorted array into groups: $A[0\cdots3]$ (starting with $a$ ), $A[4,5]$ (starting with $b$ ), $A[6, 7]$ (start with $n$ ), and $A[8]$ (starting with $n$ ).

For each group, we determine the partners (the unsorted portion) and their indices. For example, the partners of the first group are: (red denotes the sorted portion and green denotes partners)

\begin{array}{||l|l|r|r|r||} i & \text{$i$-th suffix} && i & \text{$i$-th suffix} \\ \hline 0 & bananaban & & 1 & \color{red}a\color{green}{nanaban} \\ 1 & ananaban & & 3 & \color{red}a\color{green}naban\\ 2 & nanaban & & 5 & \color{red}a\color{green}ban\\ 3 & anaban & & 7 & \color{red}a\color{green}n \\ 4 & naban & \implies& 0 & bananaban \\ 5 & aban && 6 & ban\\ 6 & ban && 2 & nanaban \\ 7 & ab && 4 & naban \\ 8 & n && 8 & n \end{array}

The key observation is that each partner is also a suffix of $T$ ! Our previous countSort has already sorted these partners as well! We put sorted indices into another array. For example, the suffix $ananaban$ is now at the $0$ -th place in the suffix array after sorting the first character, so it has value $0$ in the following table. Alternatively, we are recording where each $i$ got moved to after sorting:

\begin{array}{r|r } i& 0 & 1 & 2 & 3 & 4 & 5 & 6 & 7 & 8 \\ \hline T& b & a & n & a & n & a & b & a & n\\ B:\text{Index of $T[i\cdots n-1]$ in $A_0$}& 4 & \color{magenta}0 & 6 & 1 & 7 & 2 & 5 & 3 & 8 \end{array}

Then, we can sort by indices of partners. For example, for group 1, $nanaban$ has index $6$ , $naban$ has index $7$ , $ban$ has index $5$ , and $n$ has index $8$ . Thus, we reorder the first four entries of the suffix array to

\begin{array}{||l|l|r|r|r|r|} i & \text{$i$-th suffix} && i & \text{$i$-th suffix} & B && i & \text{$i$-th suffix} \\ \hline 0 & bananaban & & 1 & \color{red}a\color{green}{nanaban} & 6 && 5 & \color{red}a\color{green}ban\\ 1 & ananaban & & 3 & \color{red}a\color{green}naban & 7 && 1 & \color{red}a\color{green}nanaban\\ 2 & nanaban & & 5 & \color{red}a\color{green}ban & 5 && 3 & \color{red}a\color{green}naban\\ 3 & anaban & & 7 & \color{red}a\color{green}n & 8 & & 7 & \color{red}a\color{green}n\\ 4 & naban &\implies& 0 & bananaban &&\implies \\ 5 & aban && 6 & ban & \\ 6 & ban && 2 & nanaban \\ 7 & ab && 4 & naban \\ 8 & n && 8 & n \end{array}

We do the same for the rest of the suffixes. An interesting observation is that since the full string is located at $4$ after sorting, no partner would have $4$ as their index, i.e., $4$ is disappeared from column $B$ . Also, $n$ has no partner, so we give its partner $-1$ to make sure it has the smallest partner index.

\begin{array}{||l|l|r|r|r|r|} i & \text{$i$-th suffix} && i & \text{$i$-th suffix} & B && i & \text{$i$-th suffix} \\ \hline 0 & bananaban & & 1 & \color{red}a\color{green}{nanaban} & 6 && 5 & \color{red}a\color{green}ban\\ 1 & ananaban & & 3 & \color{red}a\color{green}naban & 7 && 1 & \color{red}a\color{green}nanaban\\ 2 & nanaban & & 5 & \color{red}a\color{green}ban & 5 && 3 & \color{red}a\color{green}naban\\ 3 & anaban & & 7 & \color{red}a\color{green}n & 8 & & 7 & \color{red}a\color{green}n\\ 4 & naban & \implies& 0 & \color{red}b\color{green}ananaban &1& \implies&0 &\color{red}b\color{green}ananaban\\ 5 & aban && 6 & \color{red}b\color{green}an &3&&6& \color{red}b\color{green}an\\ 6 & ban && 2 & \color{red}n\color{green}anaban &2&&8&\color{red}n \\ 7 & ab && 4 & \color{red}n\color{green}aban &0&&2&\color{red}n\color{green}anaban \\ 8 & n && 8 & \color{red}n & -1&&4& \color{red}n\color{green}aban \end{array}

Note that we need to update the auxiliary array after every countSort:

\begin{array}{r|r } i& 0 & 1 & 2 & 3 & 4 & 5 & 6 & 7 & 8 \\ \hline T& b & a & n & a & n & a & b & a & n\\ B:\text{Index of $T[i\cdots n-1]$ in $A_1$}& 4 & 1 & 7 & 2 & 8 & 0 & 5 & 3 & 6 \end{array}

We repeat this process until all suffixes are sorted:

\begin{array}{||l|l|r|r|r|r|r|r|r|} i & \text{$i$-th suffix} && i & \text{$i$-th suffix} & B && i & \text{$i$-th suffix} & B && i & \text{$i$-th suffix}\\ \hline 0 & bananaban & & 1 & \color{red}a\color{green}nanaban & 6 && 5 & \color{red}ab\color{green}an & X& & 5 & \color{red}aban \\ 1 & ananaban & & 3 & \color{red}a\color{green}naban & 7 && 1 & \color{red}an\color{green}anaban & 2 && 7 & \color{red}an\\ 2 & nanaban & & 5 & \color{red}a\color{green}ban & 5 && 3 & \color{red}an\color{green}aban & 0 && 3 &\color{red}anab\color{green}an\\ 3 & anaban & & 7 & \color{red}a\color{green}n & 8 && 7 & \color{red}an & -1 & & 1 &\color{red}anan\color{green}aban\\ 4 & naban &\Rightarrow& 0 & \color{red}ban\color{green}anaban &1&\Rightarrow&0 &\color{red}ba\color{green}nanaban & 7 &\Rightarrow& 6 &\color{red}ban\\ 5 & aban && 6 & \color{red}b\color{green}an &3&&6& \color{red}ba\color{green}n &6&& 0 &\color{red} bana\color{green}naban\\ 6 & ban && 2 & \color{red}n\color{green}anaban &2&&8&\color{red}n &X&& 8 &\color{red} n\\ 7 & ab && 4 & \color{red}n\color{green}aban &0&&2&\color{red}na\color{green}naban & 8 &&4& \color{red}naba\color{green}n\\ 8 & n && 8 & \color{red}n & -1&&4& \color{red}na\color{green}ban &5 && 2 & \color{red}nana\color{green}ban \end{array}

Observe the first countSort sorts all first digits and the second countSorts sorts one more digit in addition to that. The third time, however, since we are using the result from the second countSort which we know two digits have already been sorted, we are sorting by two more digits! In summary, at iteration $j$ , we know $A_j$ is sorted by the first $2^j$ characters, so the next iteration doubles the amount of digits that are sorted. This is because we are sorting by $B$ -values, which are indices telling us the sorted order of partners with respect to their first $2^j$ characters. When $j = \log n$ , everything is sorted.

Analysis

Building

Recall countSort uses $O(n+R)$ time and $\Theta(n)$ where $R$ is the number of digits.
Building suffix array takes $O(\log n)$ iterations of countSort, so overall the process takes $O(n\log n)$ time.

Searching

Binary search on suffix array takes $O(\log n)$ comparisons as there are $n$ suffixes for a text of size $n$ .
Each comparison is a strcmp which takes $O(m) = O(|P|)$ . Thus overall searching takes $O(m \log n)$ .

Space

Suffix array is slightly slower than suffix tree but it saves a lot of space compared to suffix tree.