Range Search

CS240E: Data Structures and Data Management (Enriched)

David Duan, 2019 Winter

Partition Trees

A tree with $n$ leaves where

• Each leaf node corresponds to an actual item, and
• Each internal node corresponds to a region.

Quadtrees

Given $n$ points $S = \{(x_0, y_0), (x_1, y_1), \ldots, (x_{n-1}, y_{n-1})\}$ in the place and assume all points are bounded by a box of the form $R = [0, 2^M) \times [0, 2^M)$¹, we construct a quadtree on $S$ as follows:

1. Root node $r$ of the quadtree $T$ corresponds to the entire region $R$.
2. If $R$ contains $0$ or $1$ points only, then root $r$ is a leaf that stores the point.
3. Otherwise, we partition $R$ into four quadrants: $R_{NE}$, $R_{NW}$, $R_{SW}$, $R_{SE}$ and insert four subtrees $T_{NE}$, $T_{NW}$, $T_{SW}$, $T_{SE}$ to the root $r$ of $T$, where each $T_i$ is associated with $R_i$.
4. We recursively repeat this process at each subtree. Note that each recursive call ends when the regions has only one or zero point inside.

Example

Given the following points in the left, we recursively partition the square into smaller regions, until each region contains at most one point, i.e., the right picture.

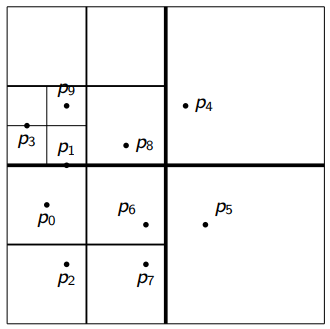
The computer stores the quadtree as shown in the left, but we could ignore the empty regions/nodes and instead label the edges.

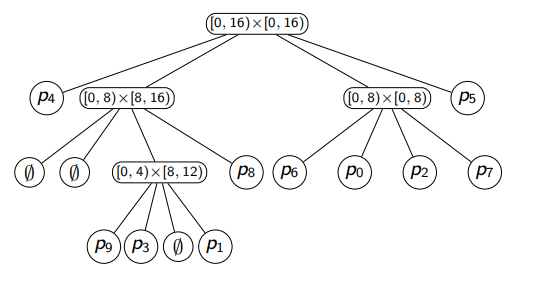
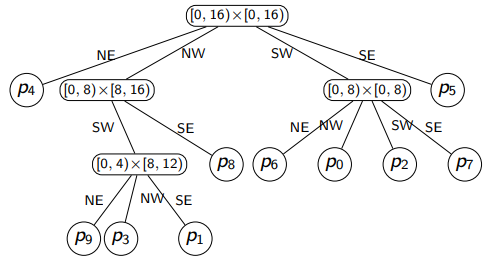
Dictionary Operations

Search: Analogous to BSTs and tries.

Insert: search for the new point (for where it should be), now split the region (repeatedly if necessary) until the new point is in a region of its own.

Range Search

Let $T$ be a quadtree, $R_T$ be the square corresponding to $T$, and $A$ be our query rectangle. We can classify nodes in the quadtree as follows:

1. Green: $T$ is green if ​$R_T$ potentially coincides with ​$A$; we need to further explore.
2. Blue: $T$ is blue if $R_T$ is disjoint with $A$; we know it cannot contain any point we want.
3. Pink: $T$ is pink if $R_T$ is a subset of $A$; every point in $R_T$ must also be in $A$.

We have four cases to deal with:

• Base Case I: If $R_T \subseteq A$, i.e., $T$ is a pink node, then every point in $R_T$ (i.e., every node in $T$) must be in $A$. We report all points in $T$ and return.
• Base Case II: If $R_T \cap A = \varnothing$, i.e., $T$ is a blue node, then every point in $R_T$ (i.e., every node in $T$) must not be in $A$. We discard them (by doing nothing) and return.
• Base Case III: Now $T$ must be green. If $|T| = 1$, i.e., $T$ contains only one node (i.e., $R_T$ contains one point), then we explicitly check if $p \in A$. We report it if yes / discard it if no and return.
• Recursion: Now $T$ is green and contains multiple nodes (i.e., $R_T$ contains multiple points). We call $RangeSearch$ on each child (i.e., search each region).

Height Analysis

Define $\beta(S)$ to be the spread factor of points in $S$:

Then the height of a quadtree is bounded by

Note that if the minimum distance between two points are small, the height could very large.

Remarks

In 3D, we have oct-trees; in 1D, we get a trie! ²

kd-Trees

Instead of blindly cutting regions into the same size (Trie), we now split the points so that the set of points is cut in roughly half (BST).

On the first cut, we use a vertical line to split the dataset according to the $x$-coordinates; on the next cut, we use a horizontal line to split each subset based on the $y$-coordinates. We repeat this procedure until every point is in its own region.

To construct a kd-Tree with initial split by $x$ on $S$:

1. If $|S| \leq 1$, create a leaf and return.
2. Else, define $X:=QuickSelect(S, \lfloor n/2\rfloor)$.
3. Partition $S$ by $x$-coordinates into $S_{x < X}$ and $S_{x \geq X}$.
4. Create left subtree recursively (splitting by $y$) for points $S_{x < X}$.
5. Create the right subtree recursively (splitting by $y$) for points $S_{x \geq X}$.

Just like quadtrees can be seen as 2D tries, kd-trees can be seen as 2D BST or decision trees.

Example

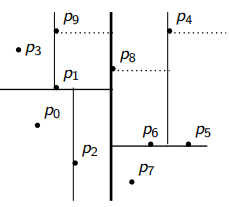
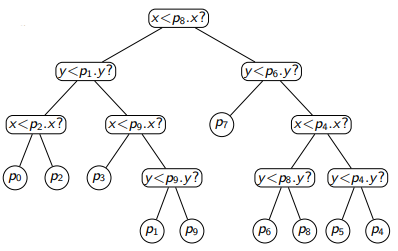
Height Analysis

Recall in construction procedure, we split along the line through the point that is $(\lfloor n/2\rfloor+1)$-th in $x$ or $y$ direction. Thus, we have at most $\lfloor n/2\rfloor$ points in the bottom/left region, but we don't have a clear bound on the right/top side as we can't guarantee how many are sitting on the median line. For example, consider the following extreme case:

Our "decision tree" built here has an infinite height, because on each level, the left subtree is always empty and the right subtree contains the same $6$ elements; the problem size doesn't decrease as we go deeper into the tree. This shows us that kd-trees have even worse performance than quadtrees in theory.

However, given the input is nice (general position, i.e., no two $x$ or $y$-coordinates are the same), if you split by the median, you are essentially creating a very balanced BST, where $\lfloor n/2 \rfloor$ points on one side and $\lceil n/2 \rceil$ the other side. Thus, the height is in $O(\log n)$.

Dictionary Operations

Search: Analogous to BSTs and tries.

Insert: To keep our height $O(\log n)$, we could track our height and rebuild a subtree after insertion if needed as in scapegoat trees.

Complexity

Build:

• Find the median ($QuickSelect$): $O(n)$ expected.
• Split the points (one pass): $O(n)$.
• Recursion: $T(n) = O(n) + 2T(n/2) \implies T(n) \in O(n \log n)$ expected.

Search: $O(h) = O(\log n)$ given the input is nice.

Insert: Amortized $O(\log n)$.

Range Search

The $RangeSearch$ procedure for kd-trees are almost identical to quadtree's:

Range Search Analysis

Recall color coding from before:

1. Green: $T$ is green if ​$R_T$ potentially coincides with ​$A$; we need to further explore.
2. Blue: $T$ is blue if $R_T$ is disjoint with $A$; we know it cannot contain any point we want.
3. Pink: $T$ is pink if $R_T$ is a subset of $A$; every point in $R_T$ must also be in $A$.

We want to show that if the points are in general position (i.e., no coinciding coordinates), then there are $O(\sqrt n)$ green nodes. It is enough to show there are $O(\sqrt n)$ nodes for which the region $R$ intersects the left side of $A$.

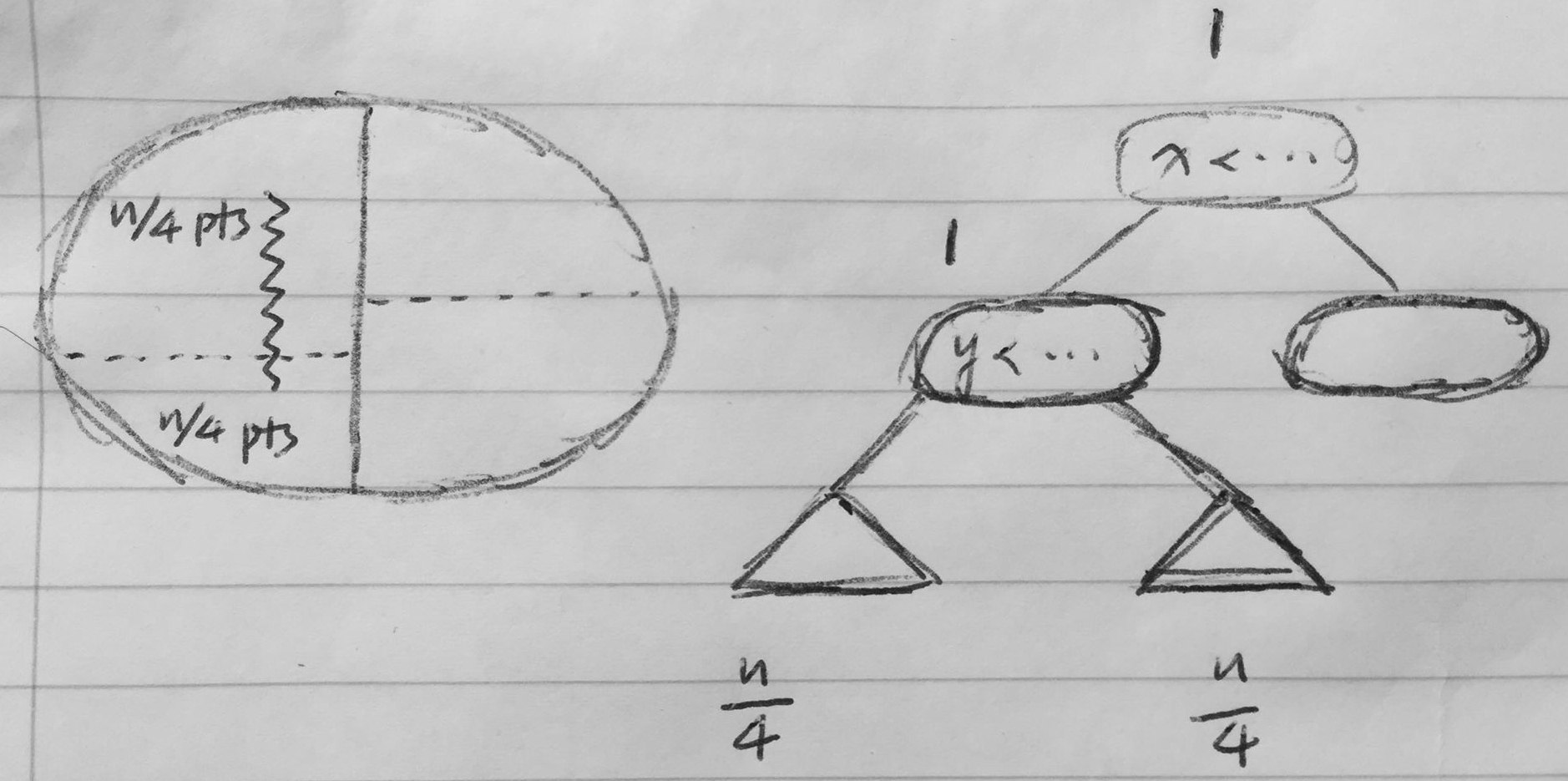
Let the squiggly line represent the left side of $A$; we want to count how many regions intersects it. During our first split, we can get rid of the right side as we know none of those nodes will intersect the line. During our second split, however, since we are cutting horizontally, we cannot guarantee one of the two sub-regions on the left side has no node intersecting the line. Thus, we must check both sub-regions next time. Therefore, we need to process $2O(n/4)$ nodes (both sub-regions on the left side) plus the $2$ green nodes we just processed (root node $x < X$ and second layer $y < Y$).

More strictly speaking, let $Q(n)$ be the number of nodes in a kd-tree that stores $n$ points whose region intersects a vertical segment. We have the following recursion:

Therefore, given the tree is balanced (i.e., the input is nice), the comlplexity of a range search in kd-trees is $O(s + \sqrt n)$ where $s$ is the size of output.

Higher Dimensions

For a $d$-dimensional space,

• At the root the point set is partitioned based on the first coordinate,
• At the second layer the partition is based on the second coordinate,
• ...
• At layer $d-1$ the partition is based on the last coordinate,
• At layer $d$ we start all over again, until each point has its own region.

Complexity (assume that $o(n)$ points share coordinates and $d$ is a constant):

• Space: $O(n)$.
• Construction: $O(n \log n)$.
• RangeSearch: $O(s + n^{1-1/d})$.

Range Trees

We now present a new data structure which provides much faster range query operation but requires more than linear space.

(Balanced) BST Range Search

Strategy

1. Search for $k_1$ in $T$: returns a path $P_1$.

2. Search for $k_2$ in $T$: returns a path $P_2$.

3. Partition nodes of $T$ into three groups:

   1. Green/boundary node: on $P_1$ or $P_2$; check each green node to see if it is in the search range.
   2. Blue: definitely not in the range, so you are either a left child in $P_1$ where $P_1$ goes right, or right child in $P_2$ where $P_2$ goes left.
   3. Pink/allocation node: $x$ coordinates are definitely in the range; the "inside nodes".

4. Report all allocation nodes; test each boundary node and report it if in range.

Example

$P_1 : 52 \to 35 \to 15 \to 27 \to 29$; $P_2 : 52 \to 35 \to 42 \to 46$.

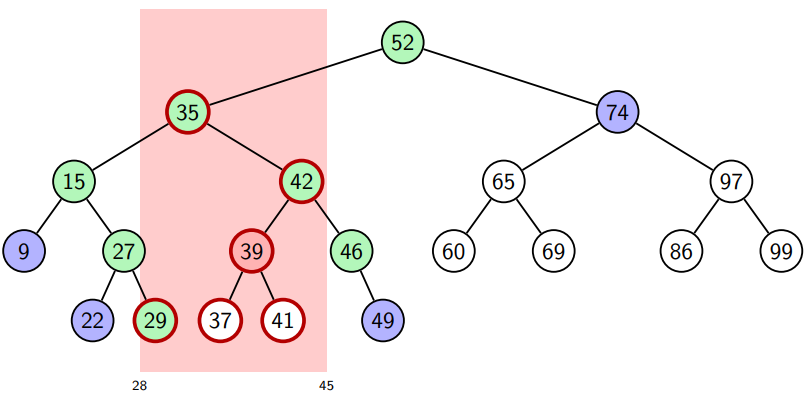
Pseudocode

The following algorithm returns keys in $T$ that are in range $[k_1, k_2]$ in sorted order.

Analysis

Assume the BST is balanced. Then $|P_1| = |P_2| = O(\log n)$ so we have $O(\log n)$ boundary nodes; testing each of them requires $O(\log n)$ time. Next, recall $v$ is an allocation node if it is not in $P_1$ or $P_2$ but its parent is (not both); if parent in $P_1$, $v$ is a right child; if parent in $P_2$, $v$ is a left child. Since query stops at the topmost level (of allocation nodes) and there are $O(\log n)$ nodes on $P_1$ and $P_2$, they take $O(\log n)$ time. Finally, reporting all $s$ results takes $O(s)$, so overall $O(\log n + s)$ time.

2D Range Trees

Given $n$ points $P= \{(x_0, y_0), (x_1, y_1), \ldots, (x_{n-1}, y_{n-1})\}$, a range tree is a tree of trees (a multi-level data structure), where

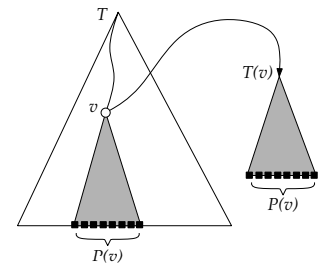
• Primary: Scapegoat Tree, called $x$-tree, as it uses $x$-coordinates as keys.
• Auxiliary: Balanced BST, called $y$-tree, as it uses $y$-coordinates as keys.

Every node in the primary data structure has an associated data structure, which contains the same set of descendents of this node, but potentially in a different order.

Space

Note that each point is in the associated data structure for all its ancestors. Since we are forcing a scapegoat tree as the primary data structure, each node has $O(\log n)$ ancestors. Thus, each node is in $O(\log n)$ associated trees. There are $n$ nodes in the primary tree, the overall auxiliary space needed is $O(n \log n)$.

Dictionary Operations

$Search((x,y))$: Search for $x$ in the primary tree $T$, $O(\log n)$ time. Note that $x$ could exists repeatedly as $x$ coordinates, so we need to solve the tie-breaking rule to find all of them. The safest choice is to compare $y$ coordinates. Then search for $y$ in the associated secondary tree, $O(\log n)$ time.

$Insert((x,y))$: Insert $x$ into the primary tree $T$, $O(\log n)$ time. For each of the $O(\log n)$ nodes on the path to the insertion point, insert to the associated $y$-tree, so overall $O(\log^2 n)$.

No Rotation in Primary Tree

We don't want to rotate the primary tree, because then the associated trees will be messed up. Because we use scapegoat trees,

1. We don't need rotations to guarantee $O(\log n)$ height,
2. When we rebuild a subtree of the primary tree, we also rebuild all associated trees of that subtree,
3. We can show the amortized time is still $O(\log^2 n)$.

Range Search

1. Do a range query by $x$-coordinates in primary tree $T$; color code each node as pink/green/blue: $O(\log n)$.
2. For each green node, explicitly test whether the point is in range: $O(\log n)$.
3. For each pink node, do a range query by $y$-coordinates; each takes $O(\log n)$ and $O(\log n)$ pinks, so overall $O(\log^2 n)$ nodes.

Thus, we can do a range query in a range tree in $O(\log^2n + s)$ time where $s$ is the output size.

Higher Dimension

Range trees can be generalized to $d$-dimensional space (time-space trade-off compared to kd-trees:)

Three-Sided Range Query

Assume we query $[x',x''] \times [y',\infty)$.

Idea I Use associated data structures.

• Primary: scapegoat tree

• Associated: binary heap (recall from A1, we could find all elements larger than $x$ in $O(1+s)$ time).

• Query:

  • Query in the primary tree by $x$. $O(\log n)$
  • For each green node, test. $O(\log n)$
  • For each red node ($O(\log n)$ of them), find all elements larger than $y'$ in the associated heap. $O(\log n(1 + s)) = O(\log n)$
  • Overall: $O(\log n + s)$, where $s$ is size of output.

• Disadvantage: wasting space.

Idea II Use treaps: combining BST with heaps.

• Only structure: treap.

• Query:

  • $BSTrangesearch(x1, x2)$ to get boundary and allocation ondes.
  • Boundary nodes: explicitly test each.
  • Allocation nodes: search in each heap.

• Disadvantage: We cannot bound the height for treaps.

Idea III Separate where the point is stored from the $x$-coordinate used for split.

• No detail for this one.